Нужно найти углы ромба, зная его диагонали.
Дано:
ABCD - ромб.
Диагональ 1 (d1) = 12 см.
Диагональ 2 (d2) = 12√3 (12 корней из 3) см.
Найти:
Углы ромба (∠A, ∠B, ∠C, ∠D = ?).
Ответы
Ответ дал:
0
ABCD - ромб.
Диагональ 1 (d1) = 12 см.
Диагональ 2 (d2) = 12√3 (12 корней из 3) см.
Приложения:
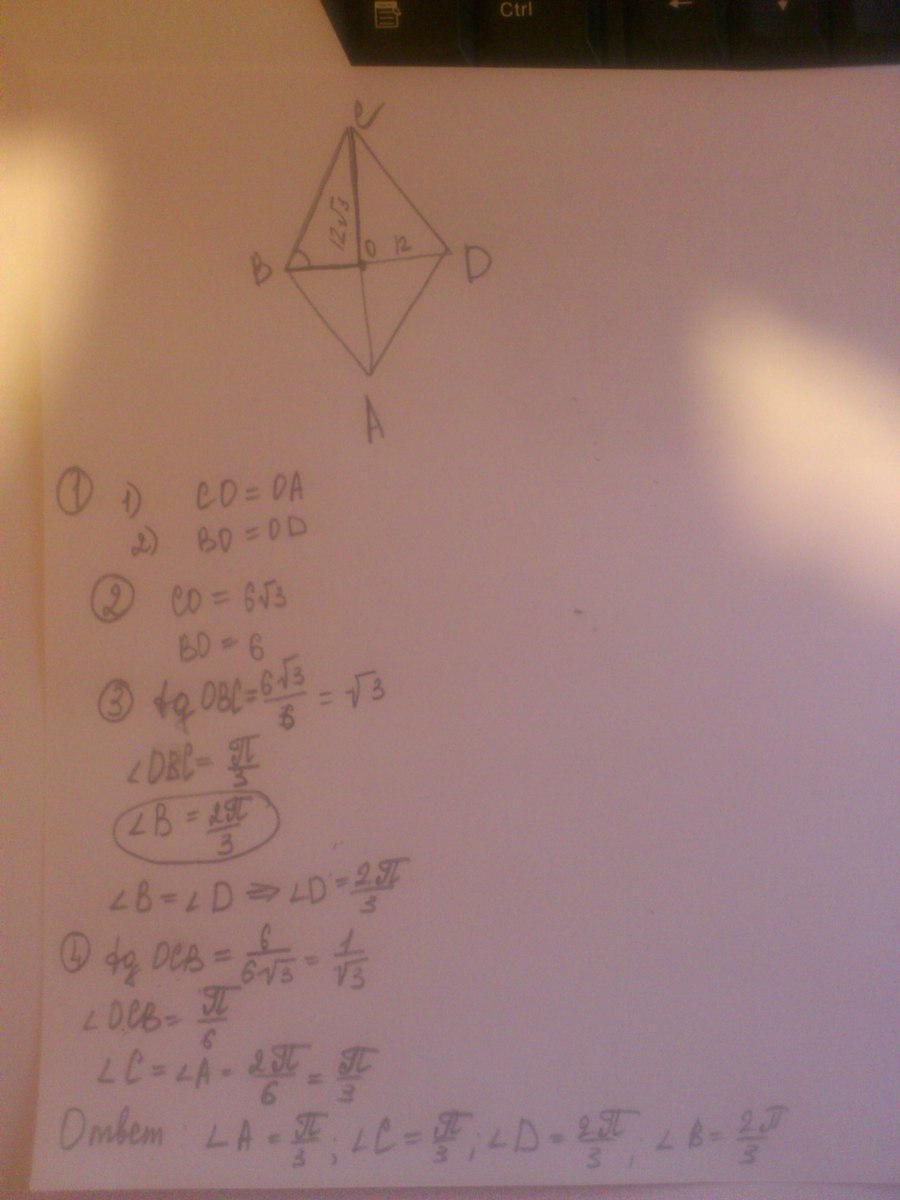
Ответ дал:
0
Диагонали ромба, пересекаясь, образуют 4 равных прямоугольных треугольников, делятся точкой пересечения пополам. Угол А=С=2arctg(6V3/6)=2*60=120 градусов, угол В=Д=(360-(2*120))/2=60 градусов, так как в выпуклом четырехугольнике сумма углов =360 градусов.
Есть и другой вариант определения углов В=Д=2arctg(6/6V3)=2*30=60 градусов.
Приложения:
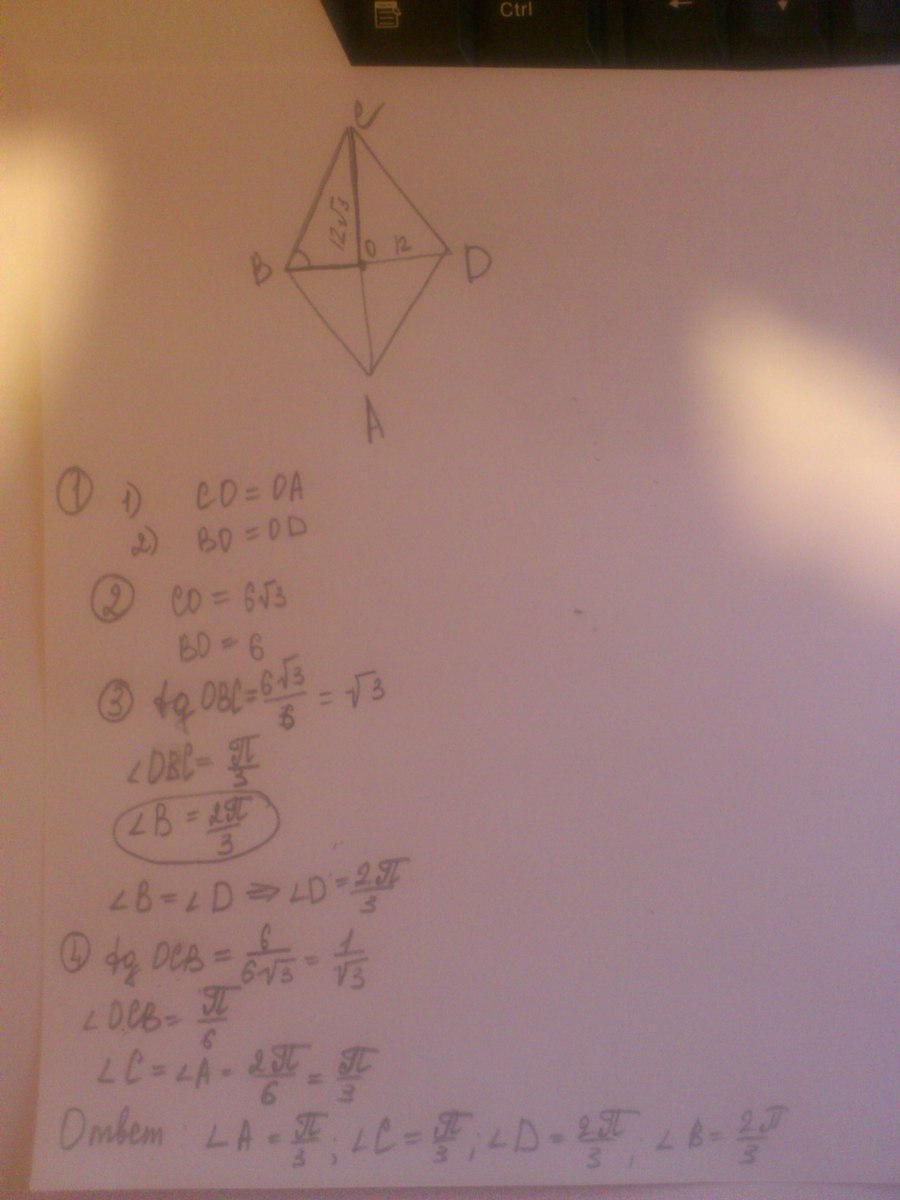
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад