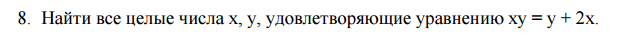Помогите пожалуйста,

Осталось установить, при каких целых значениях x правая сторона уравнения будет принимать целые значения.
Число 2x будет делиться нацело на (x - 1) только в тех случаях, когда (x - 1) равно 1, -1, 2, -2. Почему? Рассудим от противного, пусть (x-1) не равно 1, -1, 2, -2 и делит 2x, т.к. оно взаимнопросто с 2, то по известной Лемме 1, должно делить x, но, по другой известной Лемме 2, число x-1 не делит x, если x - 1 ≠ 1. Получаем противоречие.

Целые решения уравнения:

Лемма 2: (x - 1, x) = 1

(a, b) - наибольший общий делитель чисел a и b.

Если (a, b) = 1, то числа a и b - взаимнопросты. Т.е. в Лемме 2 утверждается, что целое число взаимнопросто со своими соседями.

Доказательство, вообще, можно опустить. Я его привёл для полноты решения.

Числа 2, -2, 1, -1 в ходе решения - это целые делители числа 2. Т.е. они взяты не случайно.