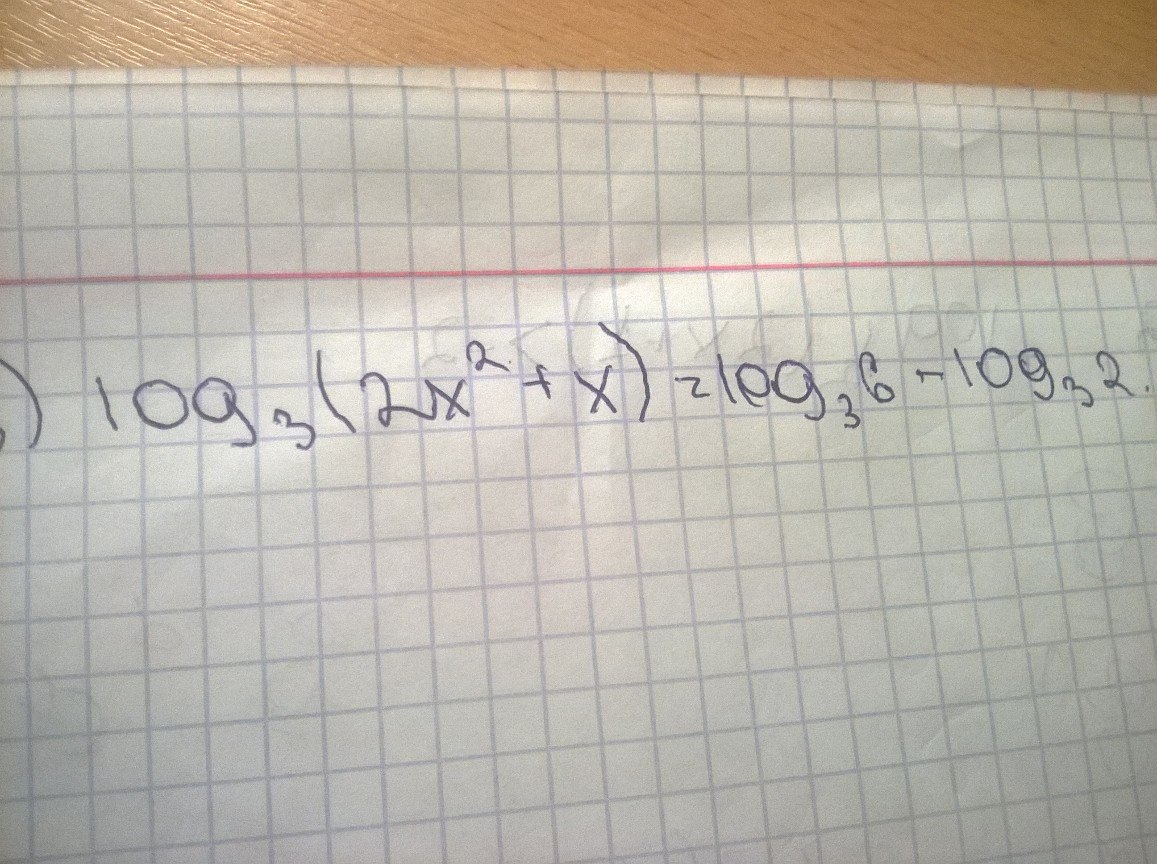Ответы
Ответ дал:
3
ОДЗ

x=0
2x+1=0
x=(-1):2
x=-0.5
+ - +
----(-0.5)------(0)-----
х∈(-∞;-0,5)∪(0;+∞);
в правой части свойство логарифмов.
основания одниковые, значит можно собрать формулу
"-" следовательно деление





проверка
1)
2*1+1 = 6/2
3 = 3
2)
2*(36/16) - 6/4 = 6/2
72/16 - 6/4 = 3
(72-24)/16 = 3
48/16 = 3
3 = 3
x=0
2x+1=0
x=(-1):2
x=-0.5
+ - +
----(-0.5)------(0)-----
х∈(-∞;-0,5)∪(0;+∞);
в правой части свойство логарифмов.
основания одниковые, значит можно собрать формулу
"-" следовательно деление
проверка
1)
2*1+1 = 6/2
3 = 3
2)
2*(36/16) - 6/4 = 6/2
72/16 - 6/4 = 3
(72-24)/16 = 3
48/16 = 3
3 = 3
WinSagit:
отметь "лучшее решение" и тебе вернутся баллы ;)
блииин.я так и думала. спасибо Вам)))
большое
пожалуйста
Похожие вопросы
1 год назад
2 года назад
2 года назад
8 лет назад