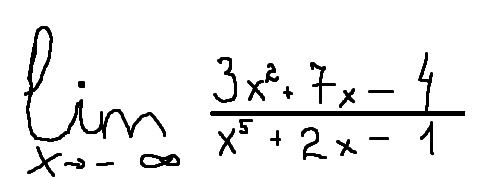Ответы
Ответ дал:
1
Стремится к - бесконечности?
![\lim_{x \to \infty} \frac{3x^2+7x-4}{x^5+2x-1}=[ \frac{0}{0}]= \lim_{n \to \infty} \frac{ \frac{3x^2}{x^5}+ \frac{7x}{x^5} - \frac{4}{x^5} }{ \frac{x^5}{x^5}+ \frac{2x}{x^5}- \frac{1}{x^5} } = \frac{0}{1} =0.](https://tex.z-dn.net/?f=+%5Clim_%7Bx+%5Cto+%5Cinfty%7D++%5Cfrac%7B3x%5E2%2B7x-4%7D%7Bx%5E5%2B2x-1%7D%3D%5B+%5Cfrac%7B0%7D%7B0%7D%5D%3D+%5Clim_%7Bn+%5Cto+%5Cinfty%7D++%5Cfrac%7B+%5Cfrac%7B3x%5E2%7D%7Bx%5E5%7D%2B+%5Cfrac%7B7x%7D%7Bx%5E5%7D+-+%5Cfrac%7B4%7D%7Bx%5E5%7D++%7D%7B+%5Cfrac%7Bx%5E5%7D%7Bx%5E5%7D%2B+%5Cfrac%7B2x%7D%7Bx%5E5%7D-+%5Cfrac%7B1%7D%7Bx%5E5%7D+++%7D+%3D+%5Cfrac%7B0%7D%7B1%7D+%3D0. "\lim_{x \to \infty} \frac{3x^2+7x-4}{x^5+2x-1}=[ \frac{0}{0}]= \lim_{n \to \infty} \frac{ \frac{3x^2}{x^5}+ \frac{7x}{x^5} - \frac{4}{x^5} }{ \frac{x^5}{x^5}+ \frac{2x}{x^5}- \frac{1}{x^5} } = \frac{0}{1} =0.")
HelenAngelo:
к минус бесконечности
Там типа все дроби в числителе и знаменателе обнуляются, кроме x^5/x^5, отсюда будет 0/1=0
Спасибо большое!
Ответ дал:
1
под знаком lim:(3+7/x-4/x^2)/(1+2/x^4-1/x^5)
без лимита ответ 3
без лимита ответ 3
Похожие вопросы
1 год назад
1 год назад
6 лет назад
6 лет назад