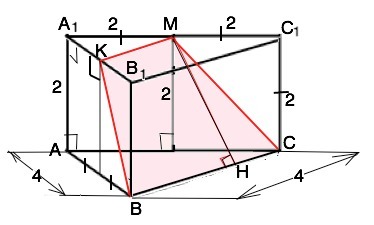
в правильной треугольной призме ABCA1B1C1 сторона основания равна 4 см. Через середину A1C1 и сторону основания BC проведена плоскость. Найдите площадь сечения, если длина бокового ребра равна 2 см.

Обозначим М середину А1С1, точку пересечения  плоскости сечения и А1В1 - К. 

Плоскости оснований призмы параллельны. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.  ⇒ КМ║ВС

 Т.М - середина А1С1. 

С1В1║СВ,  ⇒ КМ║С1В1, является средней линией ∆ А1В1С1 и равна половине С1В1. КМ=2 см. A1M=MC1=A1K=KB1=2 см

Грани правильной призмы равны. ⇒

Сечение КМСВ - равнобокая трапеция с боковыми сторонами МС и КВ. 

МС²=КВ²=MC1²+CC1²=4+4=8

Высоту МН трапеции найдем из прямоугольного ∆ МСН. 

В равнобедренной трапеции высота из тупого угла делит большее основание на отрезки, меньший из которых равен полуразности оснований, больший - их полусумме. 

СН=(ВС=КМ):2=1 см; ВН=(ВС+КМ):2=3 см 

МН=√(MC²-CH*)=√(8-1)=√7

Площадь трапеции равна произведению длины полусуммы оснований на длину высоты. 

S=3•√7 см²