Объем правильной четырёхугольной пирамиды 48, высота равна 4. найдите площадь боковой поверхности пирамиды
Ответы
Ответ дал:
18
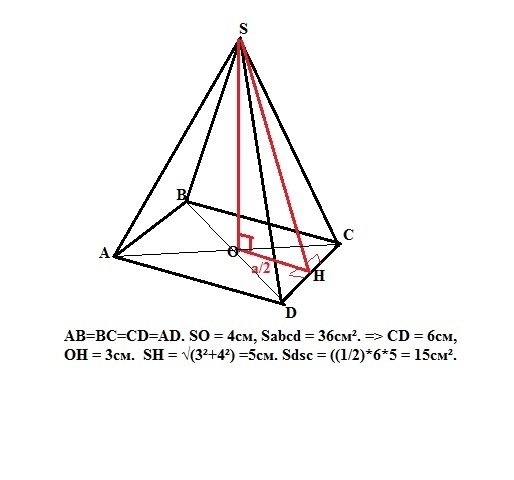
Объем пирамиды: V=(1/3)*So*H, где So - площадь основания пирамиды, H - высота пирамиды. Объем и высота нам даны, найдем площадь основания. So = 48*3/4 = 36 ед². Пирамида правильная, значит в основании лежит квадрат со стороной а = √36 = 6ед, а вершина пирамиды проецируется в центр основания - точку пересечения его диагоналей. Боковые грани нашей пирамиды - равные равнобедренные треугольники. Найдем высоту грани (апофему) из прямоугольного треугольника, образованного высотой пирамиды, половиной стороны основания (катеты) и апофемой (гипотенуза). Ап = √(3²+4²) =5ед.
Тогда площадь одной боковой грани равна Sгр=(1/2)*а*Ап или Sгр=(1/2)*6*5 = 15ед², а площадь боковой поверхности равна
Sбок = 4*Sгр. = 60 ед².
Ответ: Sбок = 60 ед².
Приложения:
Похожие вопросы
1 год назад
1 год назад
1 год назад
6 лет назад
8 лет назад