Предмет: Геометрия
Автор: sunmm
Вопрос задан 2 года назад

< >

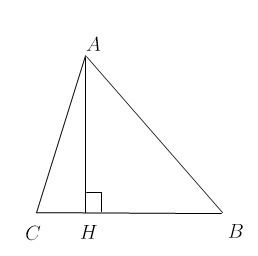
В остроугольном треугольнике ABC высота AH равна
6 корень из 39 ,
а сторона AB равна 40. Найдите cosB.

Ответы

Ответ дал: Аноним

10

Рассмотрим прямоугольный треугольник AHB в нём $AH=6\sqrt{39}$ и $AB=40$ . Найдем HB по теореме Пифагора:

$HB=\sqrt{AB^2-AH^2}=\sqrt{40^2-(6\sqrt{39} )^2}=\sqrt{40^2-36\cdot39}=14$

Косинус - отношение прилежащего катета к гипотенузе, то есть

$\cos \angle ABH=\dfrac{HB}{AB} =\dfrac{14}{40}=0.35$

Ответ: 0,35.

Приложения:

Похожие вопросы

Математика

1 год назад

8. О Найдите значение выражения: 1)0,2. (a:b), при а=8-2 и. б=1 5. 20 2) (b: a): 2-1 при а = 1 -3 Б=4-5 2 23. 23

Математика

1 год назад

(2x-1)(x²-9) = x (x²-9)

Українська мова

1 год назад

сонце+сяяти в одне слово

Русский язык

1 год назад

5 предложений, СРОЧНОООООО!!!!!

Физика

6 лет назад

№1. Стальной брусок длиной 10 см и шириной 5 см поставили на малый поршень гидравлического пресса площадью 100 см2, в результате чего на больший поршень, площадь которого 500 см2, стала

История

6 лет назад

1 расположите в хронологической последовательности: А) 1 Крещение Руси 2 Съезд князей в Любиче 3 Объединение Киева и Новгорода Б) 1 Правление Ярослава Мудрого 2 Поход Олега на Царь-град 3 Княжение

Литература

8 лет назад

Повесть Вечера на хуторе близ Диканьки. Запорожцы обращаются к царице Екатерине с просьбой. О чём они её просят? Какие исторические события здесь упоминаются? Напишите небольшой исторический

Математика

8 лет назад

У Васи марок в три раза меньше чем у Кости а вместе у них 600 марок Сколько марок у Васи И сколько у Кости