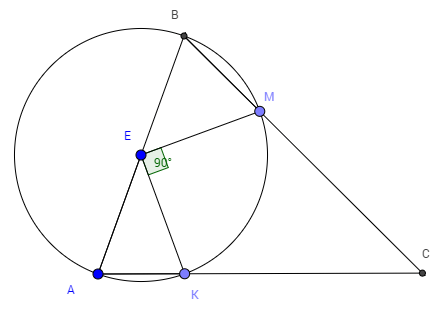
В остроугольном треугольнике АВС отрезок МК, соединяющий основания высот АМ и ВК, виден из середины Е стороны АВ под прямым углом. Найдите величину угла С.
Ответы
Ответ дал:
0
Центром окружности, описывающей прямоугольный треугольник (△AMB; △AKB), является середина гипотенузы (AB).
Точки M и K лежат на окружности диаметром AB c центром в точке E.
Угол между секущими (AC; BC) равен полуразности угловых величин дуг, заключённых в этот угол.
Угловой величиной дуги окружности является величина центрального угла, опирающегося на эту дугу.
∠С = (180°-90°)/2 = 45°
Точки M и K лежат на окружности диаметром AB c центром в точке E.
Угол между секущими (AC; BC) равен полуразности угловых величин дуг, заключённых в этот угол.
Угловой величиной дуги окружности является величина центрального угла, опирающегося на эту дугу.
∠С = (180°-90°)/2 = 45°
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад