• Предмет: Геометрия
  • Автор: Zpemik
  • Вопрос задан 2 года назад
< >

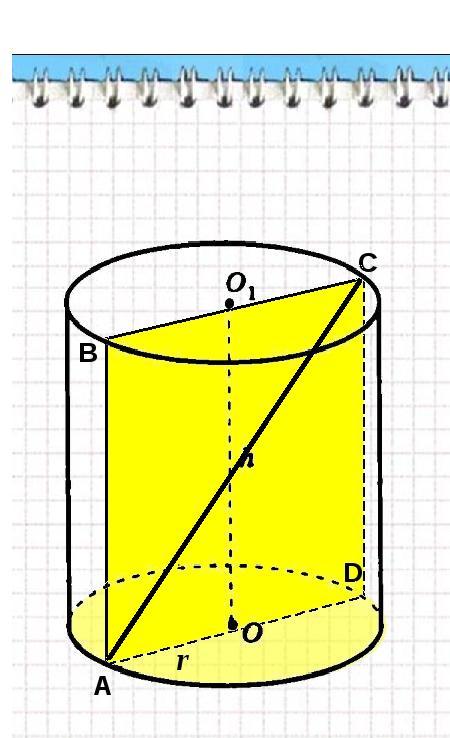
Осевое сечение цилиндра - квадрат, длина диагонали которого равна 36см. Найдите радиус основания цилиндра.
а)9см
б)8см
в)8√3см
7)9√2см

Ответы

Ответ дал: lilyatomach
8

Ответ:

решение представлено на фото

Объяснение:

Приложения:
Ответ дал: Alyssa08
11

Ответ:

r = 9\sqrt{2} см.

Объяснение:

Обозначим осевое сечение буквами ABCD.

OO_1 - высота.

AC = 36 см.

AB = BC = CD = AD, так как ABCD - квадрат.

AC = AB * \sqrt{2} = 36 см \Rightarrow AB = AC : \sqrt{2} = 36 : \sqrt{2} = 18\sqrt{2} см.

Тогда AD = 18\sqrt{2} см.

r - радиус основания цилиндра.

r = AO = OD = AD : 2 = 18\sqrt{2} : 2 = 9\sqrt{2} см.

Приложения:
Похожие вопросы
Геометрия
1 год назад
Дві сторони трикутника дорівнюють 6см і 8см, а медіана проведена до третьої сторони – 5 см. Знайди третю сторону. пж дуже терміново!! дам 30 балів!!​
Алгебра
1 год назад
срочно!!!!!!!!!!!!!!!!!!!!!!
Русский язык
1 год назад
Орфографический разбор слов "пробежал,цепочкой"
Русский язык
1 год назад
Где нужно поставить запутую в предложении В правом-лежит старинная книга в кожаном переплете и большой коричневый портфель.Даю 50 баллов!Заранее спасибо:)
Математика
6 лет назад
замени 260+660 на сумму с десятками и вычисли
Математика
6 лет назад
Помогите пожалуйста решить. Я смотрел, там не такие цифры в решении, ответ не совпадает
Математика
8 лет назад
упростите выражение 5,1 * (х-2)-3*(1,2-2) ПОДРОБНО ПОЖАЛУЙСТА НАПИШИТЕ!!!!
Биология
8 лет назад
Відповідь на подразнення за участі нервової системи називається : а. Таксисом б. Рефлексом в. Тропізмом г. Подразливістю