угол при вершине равнобедренного треугольника равен 120 градусов Боковая сторона 2 сантиметров найдите радиус описанной окружности

Треугольник АВС равнобедренный, следовательно, углы при АС равны (180°-120°):2=30°

По т.синусов

АВ:sin30°=2R

2R=2:1/2=4

R=2 см

--------

Вариант решения:

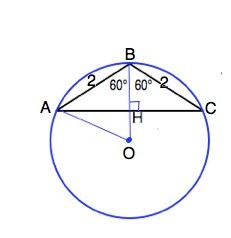
Соединим вершину В с центром окружности О. 

Т.к. центр описанной окружности лежит на срединном перпендикуляре, ВО⊥АС. ВН-высота и биссектриса ∆ АВС  и  делит угол АВС пополам. 

∠АВО=120°:2=60° 

Углы при основании равнобедренного треугольника АОВ равны. ⇒

 ∆ АОВ - равносторонний. R=AB=2 см.