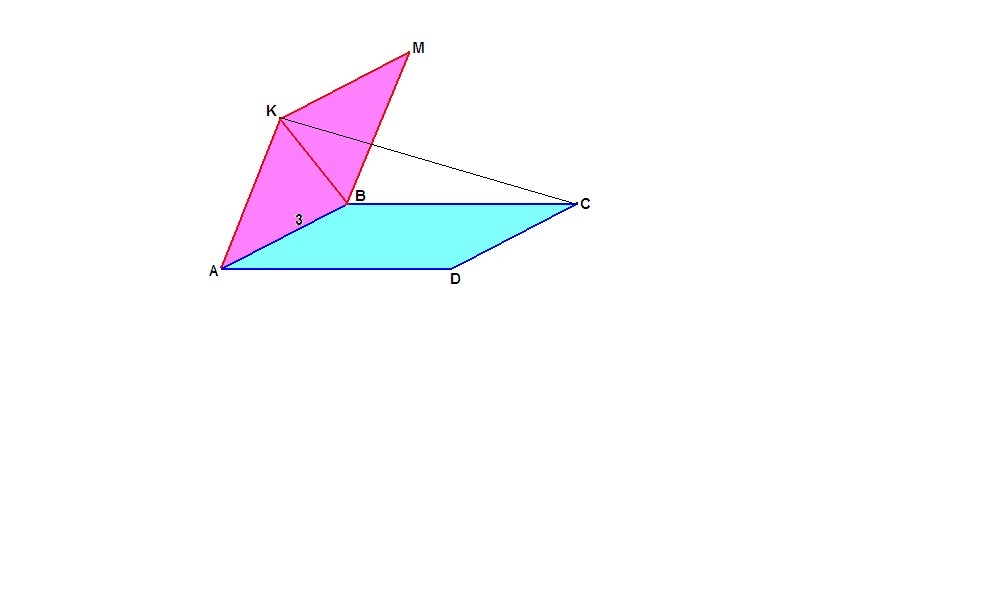
Плоскости квадрата ABCD и ромба ABMK взаимно перпендикулярны.Найдите длину СК,если сторона ромба равна 3 см,а его острый угол равен 60 градусов

Если острый угол ромба равен 60°, то его меньшая диагональ равна стороне, так как ΔАКВ равнобедренный (АВ = АК как стороны ромба) с углом 60° при вершине, значит углы при основании тоже равны  по 60°
((180° - 60°)/2 = 60°), значит он равносторонний.
КВ = АВ = 3 см.
Отрезок ВС перпендикулярен линии пересечения перпендикулярных плоскостей - АВ, значит он перпендикулярен плоскости ромба, а следовательно, и любой прямой, лежащей в этой плоскости.
ВС⊥КВ.
ΔВСК: ∠СВК = 90°, по теореме Пифагора
             КС = √(КВ² + ВС²) = √(9 + 9) = 3√2 см