сформулируйте и докажите теорему об отношении площадей подобных треугольников, оч надо

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

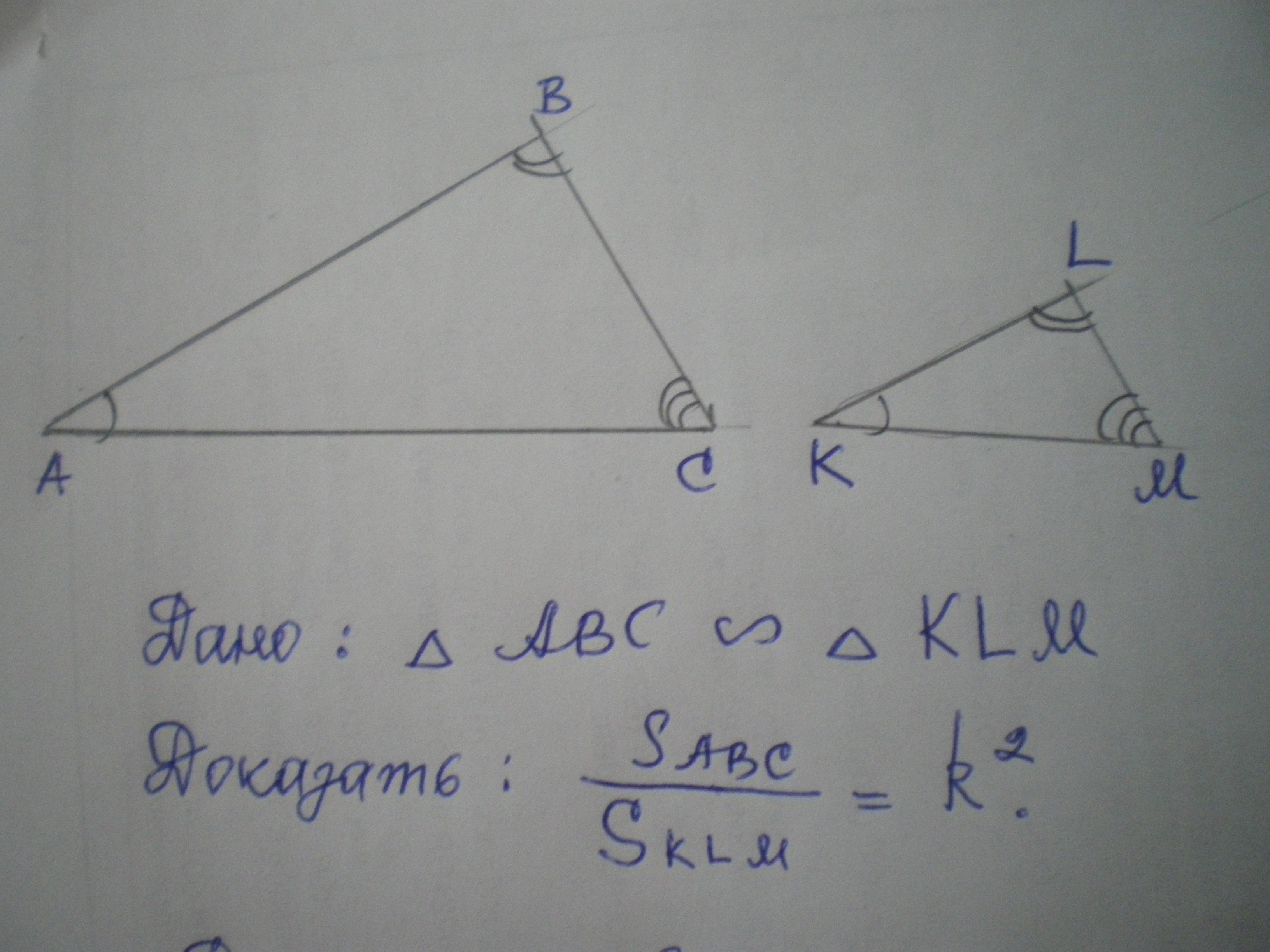
Дано: ΔАВС подобен ΔКLМ.

Доказать: S(ABC)S(KLM)=k²

Смотри чертеж.

Доказательство: из подобия треугольников следует, что АВКL=ВСLМ=АСКМ=k

Известно, что, если у двух треугольников равны углы, то их площади относятся как произведения сторон, заключающих данные углы, т.е.

S(ABC)S(KLM)=(AB*AC)(KL*KM)=ABKL * ACKM = k * k = k².

Теорема доказана.

Д