найти площадь равнобокой трапеции, меньшее основание которой равно 7 см, боковая сторона 10см, а угол при большем основании 60градуса
Ответы
Ответ дал:
0
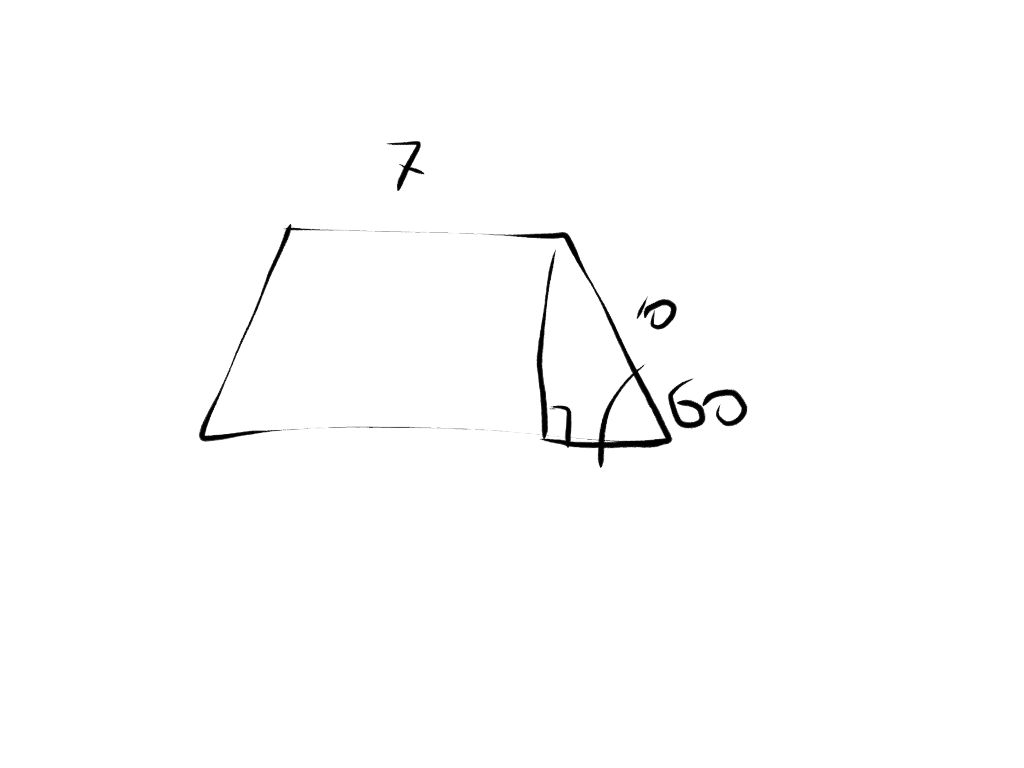
Проведем высоту трапеции из угла, который находится рядом с меньшим основанием. Получаем прямоугольный треугольник, в котором гипотенуза -сторона трапеции, один катет - высота, а второй - половинка разницы оснований.
Тогда h=sin60*10=10√3/2, а половинка разницы оснований
cos60*10=10*1/2=5
Площадь трапеции
S=h(a+b)/2
a=7
b=7+5+5=17
S=60√3
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад