RS=9см PQ=15 см SQ=8 см найти PR?

Прямые RS и PQ перпендикулярны к одной плоскости и пересекают её в точках S и Q. Найдите длину PR, если |RS| = 9 см, |РQ| = 15 см и |SQ| = 8 см.

=============================================================

Данная задача имеет два случая:

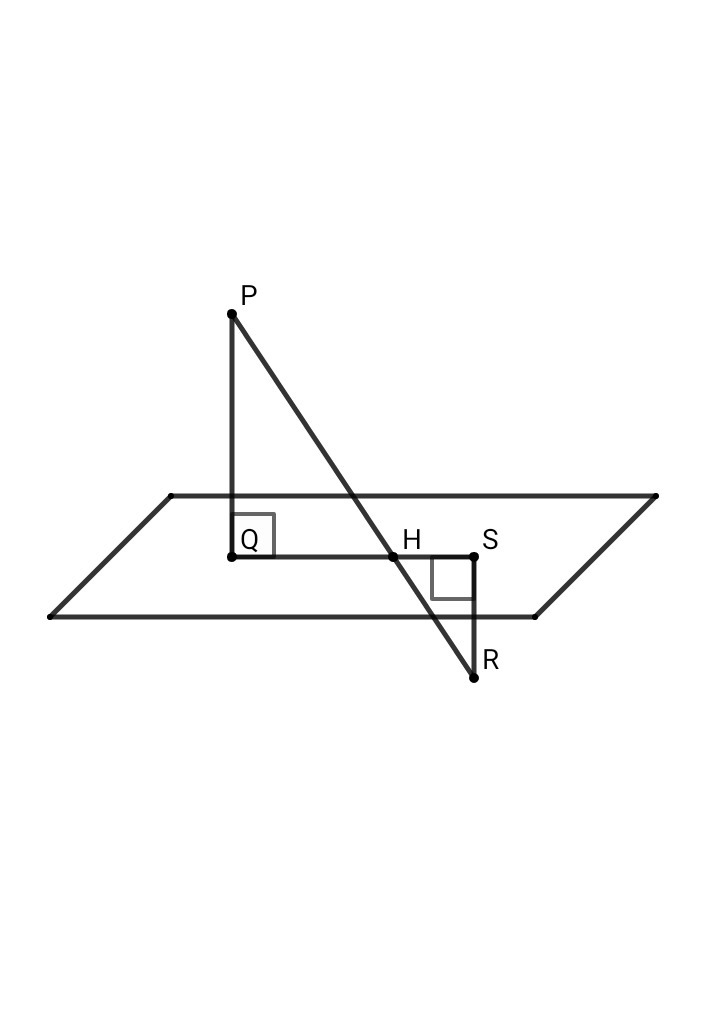
1. Точки P и R лежат по разные стороны плоскости:

PQ⊥QS , RS⊥QS  ⇒  PQ || RS

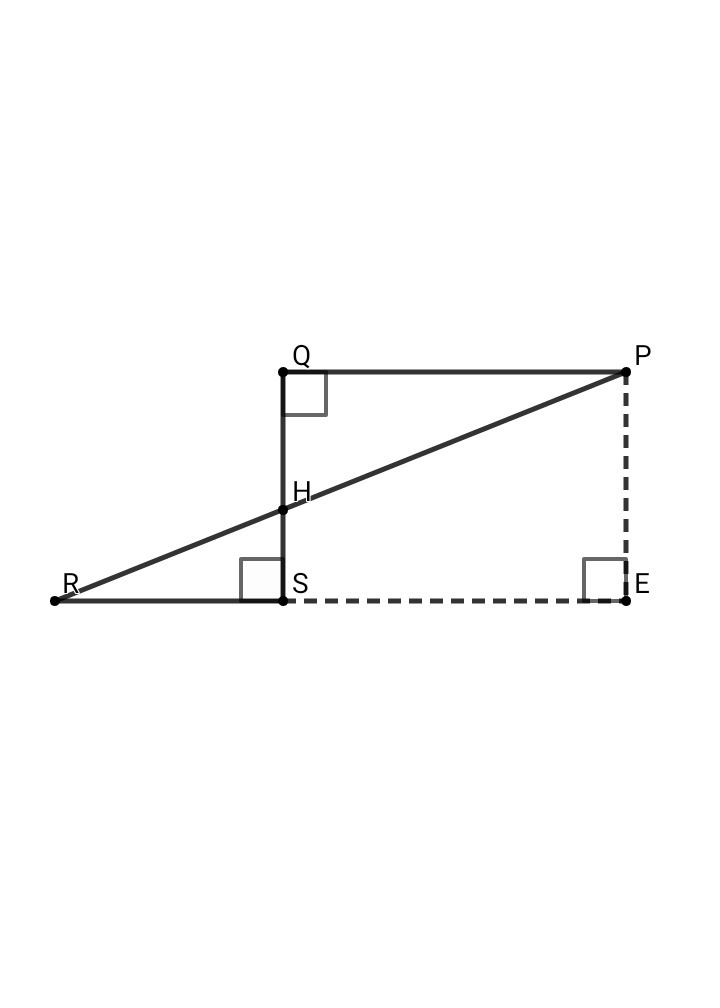
Опустим из точки Р перпендикуляр РЕ на прямую RS  ⇒  PE = QS = 8 см , SE = QP = 15 см , RE = RS + SE = 9 + 15 = 24 см

В ΔРЕR по теореме Пифагора:

PR² = RE² + PE² = 24² + 8² = 576 + 64 = 640

PR = 8√10 см

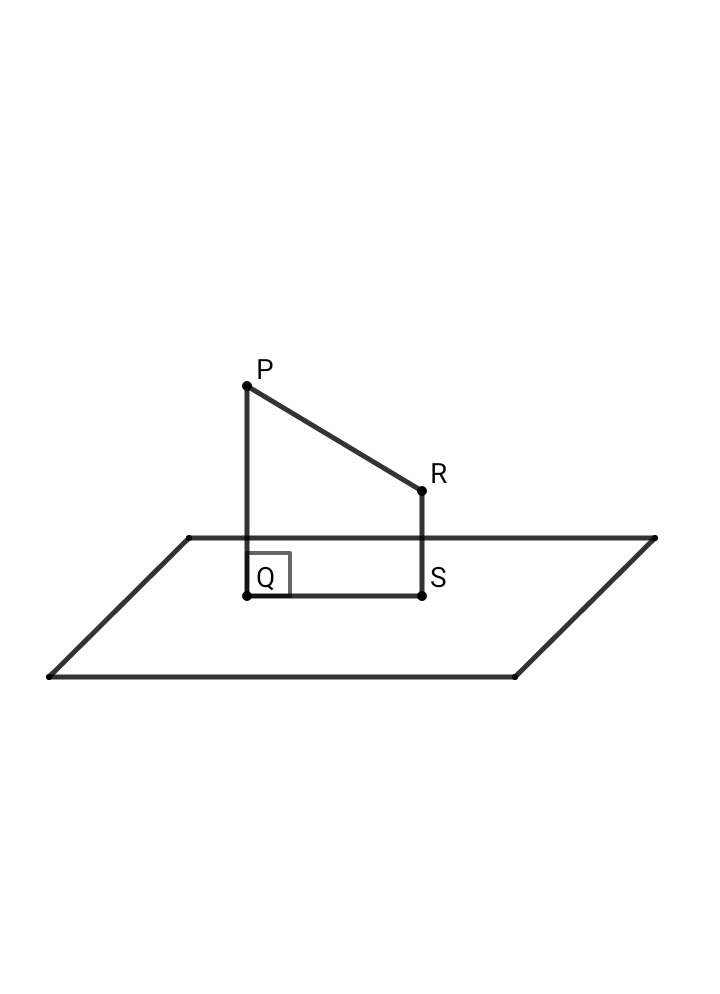
2.  Точки P и R лежат по одну сторону плоскости:

PQ⊥QS , RS⊥QS  ⇒  PQ || RS

QPRS - прямоугольная трапеция

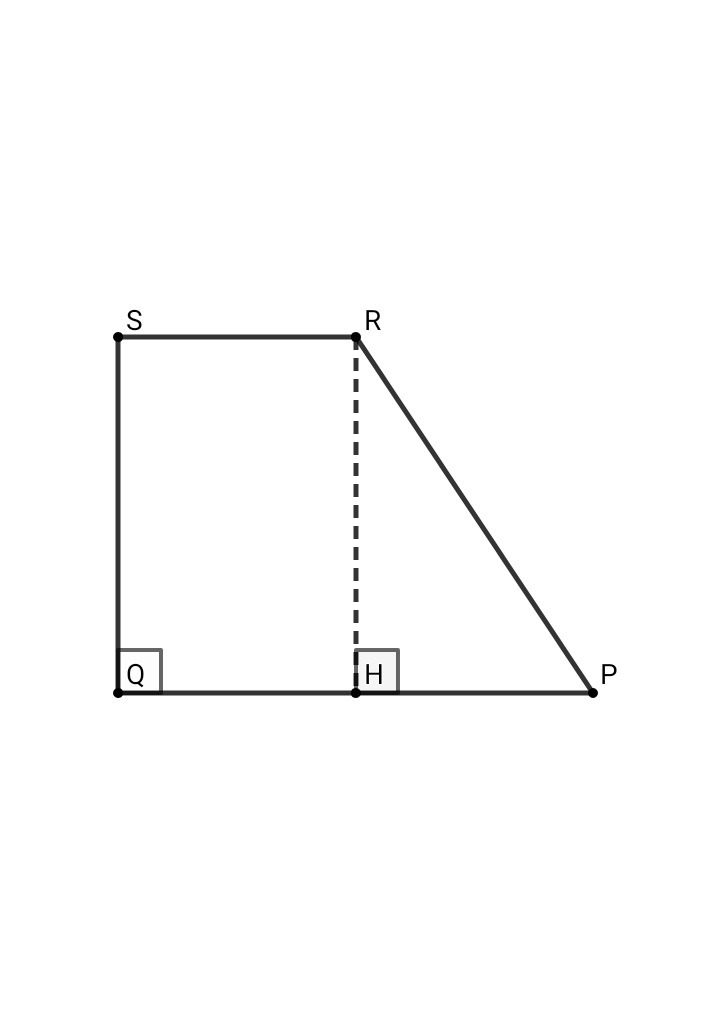
Опустим из точки R перпендикуляр RH на прямую QP ⇒  RS = QH = 9 см, НР = QP - QH = 15 - 9 = 6 см

В ΔRHP по теореме Пифагора:

RP² = RH² + HP² = 8² + 6² = 64 + 36 = 100

RP = 10 см

ОТВЕТ: 8√10 см ИЛИ 10 см