В равнобедренном треугольнике АВС со сторонами АВ =BC=8 вершины А, В середина стороны ВС и точка пересечения высот лежат на одной окружности. Найдите площадь треугольника АВС

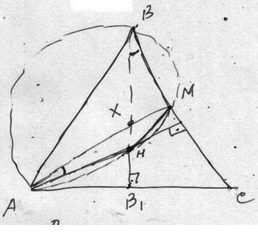
Пусть М-середина BC,Н - точка пересечения высот , Х-точка пересечения медиан, ВВ1-высота.
∠АМС=90°- ∠ НВС=∠ АСВ,треугольник АМС-равнобедренный(∠АСМ=∠АМС)
АМ=АС=α, АХ=(2α)/3, АВ1=α/2, cos ∠MAC=34
sin∠ABC=sin∠MAC=√74
S=(AB·BC·SIN∠ABC)2

Спасибо большое)