Помогите пожалуйста!!!
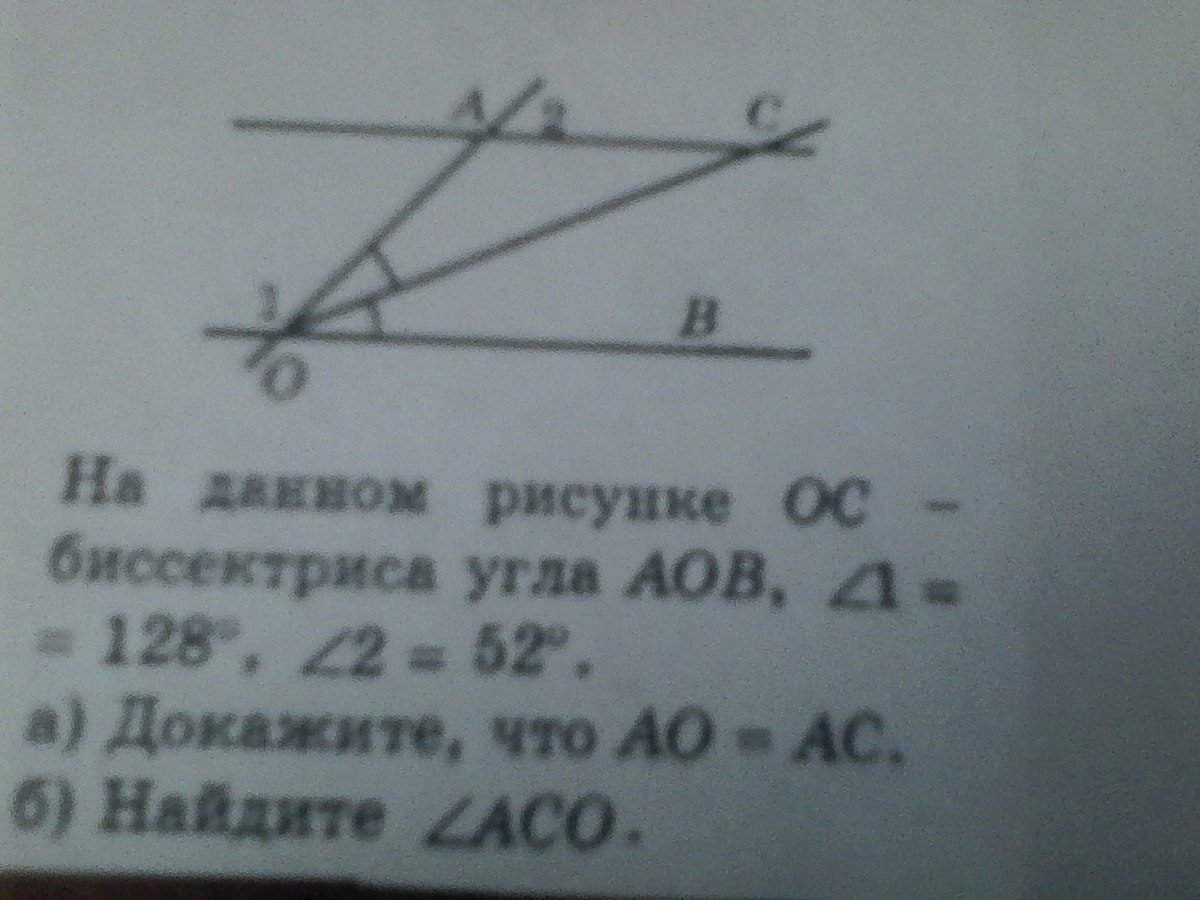
На данном рисунке ОС - биссектриса угла АОВ, угол1= 128 градусам, а угол2= 52 градусам. а) докажите, что АО = АС б) Найдите угол АСО

Из условия и рисунка:
∠2 = 180 - ∠1 ⇒ прямые AC и OB параллельны.
Из определения биссектрисы  ⇒ ∠ACO = 1/2 ∠AOB.
∠AOB = ∠2 как соответствующий
∠ACO = 1/2 * 52° = 26°
Рассмотрим ΔACO:
∠COA = ∠CAO ⇒ ΔAOC равнобедренный с основанием OC. В равнобедренном треугольнике боковые стороны равны. ЧТД.
Ответ: ∠ACO = 26°

Спасибо)