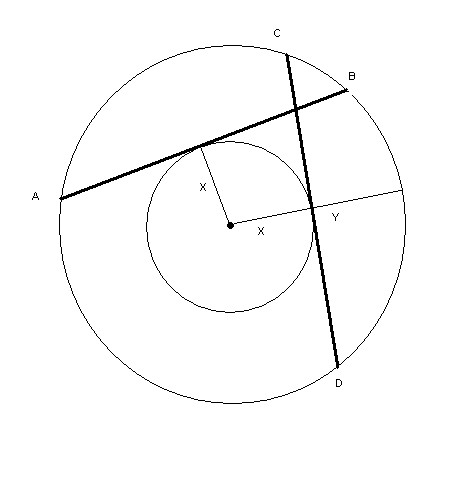
Две окружности имеют общий центр. Докажите, что хорды большей окружности, касающиеся меньшей окружности, равны между собой.
Ответы
хорды касаются меньшей, т.е. они перпедикулярны ее радиусу. Рассматриваем два равнобедренных треугольника, где боковые стороны - радиусы большей окружности, а основания - ее хорды. Высоты к основанию в этих треугольниках равны, значит равны и их основания (высота - медиана и бисектрисса): зз прямоугольных треугольников с равными и гипотенузами и общим катетом вторые катеты равны, они и есть половины оснований
Радиус большой окружности = X+Y
Радиус маленькой = Х
AB и CD- хорды,
Х перпенд. к хордам т.к касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.(св-во касательной)=>
Х- расстояние от центра окружности до хорды.
Многим в школах обьясняют что хорды ровны, если расстояние от центра окружности к хордам ровны, а у нас расстояние равно радиусу маленькой окружности=> хорды ровны)