Ребят, а как такие логарифмические неравенства решаются??? Просто не понятно, когда основания разные...
Приложения:
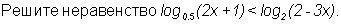
Ответы
Ответ дал:
0
log_2^(-1) (2x+ 1) <log_2 (2 - 3x)
- log_2 (2x+ 1) <log_2 (2 - 3x)
log_2 (2x+ 1) > log_2 1/(2 - 3x)
ОДЗ
2x + 1> 0
2 - 3x > 0
Имеем (1)
2x + 1 > 1/(2 - 3x)
ОДЗ
x > - 0,5
x <2/3
Получим (2)
x > 2/3; - 1/3 < x < 1/2;
Находим общее решение + ОДЗ
x ∈ ( - 1/3; 1/2)
Ответ:
x ∈ ( - 1/3; 1/2)
- log_2 (2x+ 1) <log_2 (2 - 3x)
log_2 (2x+ 1) > log_2 1/(2 - 3x)
ОДЗ
2x + 1> 0
2 - 3x > 0
Имеем (1)
2x + 1 > 1/(2 - 3x)
ОДЗ
x > - 0,5
x <2/3
Получим (2)
x > 2/3; - 1/3 < x < 1/2;
Находим общее решение + ОДЗ
x ∈ ( - 1/3; 1/2)
Ответ:
x ∈ ( - 1/3; 1/2)
Ответ дал:
0
Ну, это Вы получается нашли ОДЗ, а не само решение, увы
Ответ дал:
0
Спасибо большое.
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад
10 лет назад