• Предмет: Геометрия
  • Автор: pyma2009
  • Вопрос задан 10 лет назад
< >

меньшая диагональ правильного шестиугольника равна 5 квадратных корней из 3 см . найдите периметр шестиугольника .

Ответы

Ответ дал: as11111
0

Угол правильного шестиугольника определим по формуле:

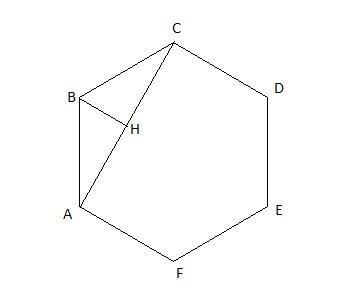
widehat{ABC}=180*frac{n-2}{n}=180*frac{6-2}{6}=120

Т.к. ΔABC равнобедренный, то ∠BAC = ∠BCA = 60° / 2 = 30°

Опустим высоту BH на основание AC равнобедренного ΔABC.

Одновременно она будет и медианой, т.е.:

AH=frac{AC}{2}=frac{5sqrt{3}}{2}

Из прямоугольного ΔABH:

AB=frac{AH}{cos{widehat{BAC}}}=frac{frac{5sqrt{3}}{2}}{cos{30}}=5

Находим периметр правильного шестиугольника:

P=5*6=30

Приложения:
Похожие вопросы
Английский язык
2 года назад
Раскройте скобки, употребив глагол в нужной форме. Secretary: Mr.Smirnov, this (to be) Mr.Gray to see you. Gray: How do you do, Sir? Smirnov:  How do you do, Mr.Gray. Will you down, please?
Қазақ тiлi
2 года назад
Помогите составить рассказ про зиму Срочко: Наступила зима. Появились первый тающие снежинки. Сегодня погода очень хорошая и тёплая. Мои друзья вышли на улицу играть в снежки, кататся на санках,
Математика
7 лет назад
Помогите пожалуйста Не могу решить
История
7 лет назад
во что объединялись купцы,ремесленники,горожане в средневековье
Алгебра
10 лет назад
Вычислите площадь фигуры,ограниченной линиями y=4/x,y=4,x=4 Очень нужно до завтра(
Химия
10 лет назад
Пожаааалуйстаааа... По термохимическому уравнению реакции: S+O2=SO2+297 кДж вычислите кол-во теплоты, которое используется при сжигании 64 г серы.
Алгебра
10 лет назад
)определите при каких значениях х, значение выражения х3 больше значения выражения 2х+64    на 1
Геометрия
10 лет назад
Постройте треугольник по стороне, прилежащему к ней углу и высоте, проведенной к этой стороне.