Помогите очень срочнооо нужн опожалуйстаааааа"

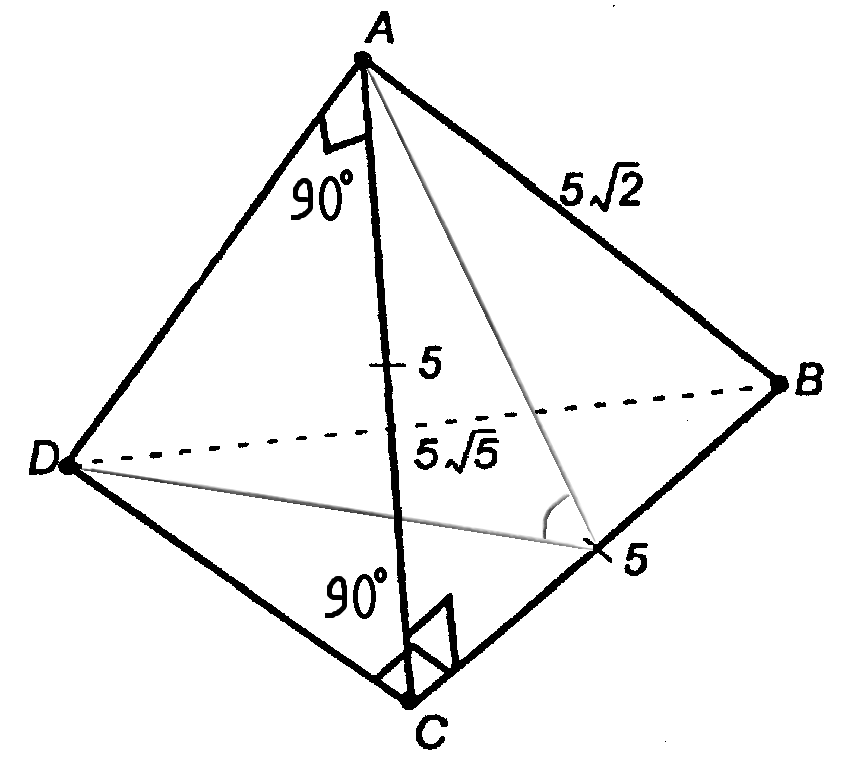
Дано: АВСD - тетраэдер; ∠DAC = ∠ACB = 90°; AC = CB = 5; DB = 5√5.

Найти: Двугранный угол ABCD.

Решение: Построим линейный угол двугранного угла ABCD. АС ⊥ СВ по условию (так как углы между ними прямые), следовательно, надо найти еще один отрезок, перпендикулярный СВ. Нам по условию даны несколько прямоугольных треугольников; подсчитаем остальные ребра тетраэдра по теореме Пифагора:

BC ⊥ AC, BC ⊥ DC, то по признаку перпендикулярности прямой и плоскости ВС ⊥ пл. ADC, следовательно, ∠ACD - линейный угол двугранного угла ABCD.

cos ∠ACD = AC/DC = ½

∠ ACD = arccos ½ = 60°.

Ответ: 60°.