Площадь боковой поверхности правильной шестиугольной пирамиды равна 192 см (квадратных), её высота равна 4 см, а апофема пирамиды конгруэнтна стороне основания. Вычислите объем пирамиды.
Ответы
Ответ дал:
0
S(бок) = 1/2 Р*h. h - это апофема пирамиды( равна а).
192 = 1/2*6а * а.
192 = 3а²
а = 8. Это сторона шестиугольника. Его площадь равна 3а²√3/2 = 3*64*√3/2 = 96√3.
v = 1/3 * 96√3 *4 = 128√3√ cм³.
192 = 1/2*6а * а.
192 = 3а²
а = 8. Это сторона шестиугольника. Его площадь равна 3а²√3/2 = 3*64*√3/2 = 96√3.
v = 1/3 * 96√3 *4 = 128√3√ cм³.
Ответ дал:
0
Лишний знак корня в конце выражения.
Ответ дал:
0
можно рисунок?
Ответ дал:
0
А что рисовать? На рисунок нигде не ссылаемся. Одни формулы.
Ответ дал:
0
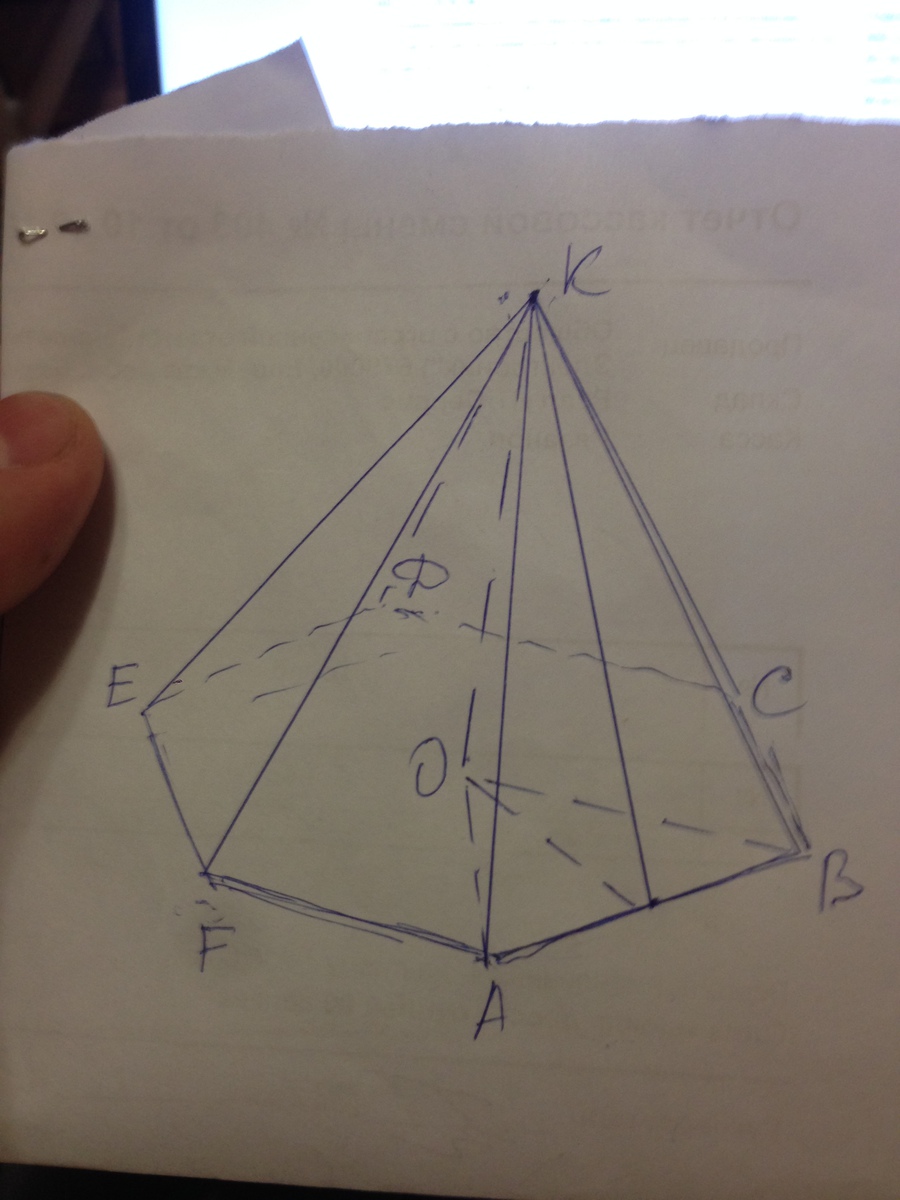
АВСДЕФК - пирамида с вершиной К. КО=4см - высота. КМ - апофема.
М∈АВ.
Боковая поверхность правильной шестиугольной пирамиды состоит из шести равнобедренных тр-ков, равных ΔАВС, следовательно площадь одного тр-ка: S3=Sбок/6=192/6=32 см².
Апофема в тр-ке АВС представляет собой высоту, опущенную на основание. КМ=АВ.
S3=КМ·АВ/2=АВ²/2,
АВ=√(2·S3)=8 см.
Площадь правильного шестиугольника, находящегося в основании, состоит из шести правильных тр-ков. Площадь одного рассчитывается по формуле S=a²√3/4
Sш=6·S=3a²√3/2=96√3 см²
V=Sш·КО/3=128√3 см³.
М∈АВ.
Боковая поверхность правильной шестиугольной пирамиды состоит из шести равнобедренных тр-ков, равных ΔАВС, следовательно площадь одного тр-ка: S3=Sбок/6=192/6=32 см².
Апофема в тр-ке АВС представляет собой высоту, опущенную на основание. КМ=АВ.
S3=КМ·АВ/2=АВ²/2,
АВ=√(2·S3)=8 см.
Площадь правильного шестиугольника, находящегося в основании, состоит из шести правильных тр-ков. Площадь одного рассчитывается по формуле S=a²√3/4
Sш=6·S=3a²√3/2=96√3 см²
V=Sш·КО/3=128√3 см³.
Приложения:
Ответ дал:
0
у меня вообще ответ в учебнике 256 корней из 3
Ответ дал:
0
Выкинь его.
Ответ дал:
0
ответ правильный
Ответ дал:
0
Безусловно.
Ответ дал:
0
ни х_у_я
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад