Предмет: Алгебра
Автор: Pandoritta
Вопрос задан 9 лет назад

< >

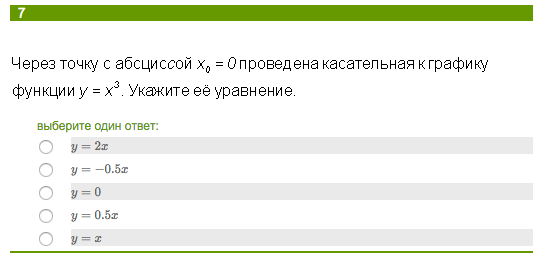
Через точку с абсциссой x0=0 проведена касательная к графику функции y=x^3. Укажите её уравнение.
С решением

Приложения:

Ответы

Ответ дал: yellok

0

Уравнение касательной к графику функции y=f(x) в точке $x_{0}$ : $y = f( x_{0} ) + f '( x_{0} )(x- x_{0} )$
$f(x)= x^{3}$
$f( x_{0} )=f( 0 )= 0^{3} =0$
$f'( x )=3* x^{3-1} =3* x^{2}$
$f'( x_{0} )=f'(0 )=3* 0^{2} =0$
значит Уравнение касательной к графику функции y=x³ будет: $y=0+0(x-0)=0$ , то есть ось абсциса

Похожие вопросы

Русский язык

2 года назад

7 слов с парными согласными в середине слова

Математика

2 года назад

решите задачу уравнением. в 2ух кусках 112 метров ткани. В первом куске в 3 раза больше метров ткани чем во втором. Сколько метров ткани во втором куске? 12 баллов

Математика

7 лет назад

из двух пунктов , расстояние которыми 370 км , вышли навстречу дргу другу одновременно два поезда. Скорость одного из них на 5км/ч больше скорости другого.Найдите скорости поездов , если известно что

Математика

7 лет назад

ДАЮ 100 БАЛЛОВ как вычислить устно 1234*1234-1234*234

Математика

9 лет назад

периметр равностороннего треугольника 24 см найди периметр квадрата сторона которого на 3 см больше стороны треугольника.

Математика

9 лет назад

проверьте, верно ли выделены целая и дробная части числа.Если задание выполнено неверно ,приведите справа верное решение .1)дробь 9/5= 1целый 4/5 2)17/4= 3целых 1/4 . 3)31/7=3 целых 4/7 4)

Информатика

10 лет назад

Составить программу для нахождения суммы первых шести чисел.

Химия

10 лет назад

Дайте название солям , формулы которых приведены ниже : BaF2 , CaCO3 , Pb3(PO4)2 , Al(NO3)3 , Li2S , K2SiO3 , Na2SO3 , CuCl2 , CuS