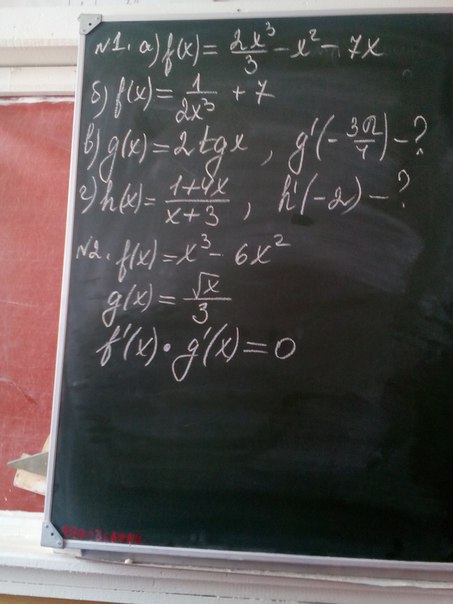Ответы
Ответ дал:
0
1.
а)
![f(x)= frac{2}{3}x^3-x^2-7x \
f'(x)= frac{2}{3}*3x^2-2x-7=2x^2-2x-7](https://tex.z-dn.net/?f=f%28x%29%3D+frac%7B2%7D%7B3%7Dx%5E3-x%5E2-7x+%5C+%0Af%27%28x%29%3D+frac%7B2%7D%7B3%7D%2A3x%5E2-2x-7%3D2x%5E2-2x-7++ "f(x)= frac{2}{3}x^3-x^2-7x \
f'(x)= frac{2}{3}*3x^2-2x-7=2x^2-2x-7")
б)
![f(x)= frac{1}{2x^3}+7= frac{1}{2}x^{-3}+7 \
f'(x)= frac{1}{2}*(-3x^{-4})=- frac{3}{2x^4}](https://tex.z-dn.net/?f=f%28x%29%3D+frac%7B1%7D%7B2x%5E3%7D%2B7%3D+frac%7B1%7D%7B2%7Dx%5E%7B-3%7D%2B7+%5C+%0Af%27%28x%29%3D+frac%7B1%7D%7B2%7D%2A%28-3x%5E%7B-4%7D%29%3D-+frac%7B3%7D%7B2x%5E4%7D+++ "f(x)= frac{1}{2x^3}+7= frac{1}{2}x^{-3}+7 \
f'(x)= frac{1}{2}*(-3x^{-4})=- frac{3}{2x^4}")
в)
g(x)=2tgx
![g'(x)= frac{2}{cos^2x} \ \
g'(- frac{3 pi }{4} )= frac{2}{cos^2(- frac{3 pi }{4} )}= frac{2}{cos^2( frac{3 pi }{4} )}= \ \
= frac{2}{cos^2( pi - frac{ pi }{4} )}= frac{2}{(-cos frac{ pi }{4} )^2}= \ \
= frac{2}{(- frac{ sqrt{2} }{2} )^2}= frac{2}{ frac{2}{4} }= frac{2*4}{2}=4](https://tex.z-dn.net/?f=g%27%28x%29%3D+frac%7B2%7D%7Bcos%5E2x%7D+%5C++%5C+%0Ag%27%28-+frac%7B3+pi+%7D%7B4%7D+%29%3D+frac%7B2%7D%7Bcos%5E2%28-+frac%7B3+pi+%7D%7B4%7D+%29%7D%3D+frac%7B2%7D%7Bcos%5E2%28+frac%7B3+pi+%7D%7B4%7D+%29%7D%3D+%5C++%5C+%0A%3D++++frac%7B2%7D%7Bcos%5E2%28+pi+-+frac%7B+pi+%7D%7B4%7D+%29%7D%3D+frac%7B2%7D%7B%28-cos+frac%7B+pi+%7D%7B4%7D+%29%5E2%7D%3D+%5C++%5C+%0A%3D+frac%7B2%7D%7B%28-+frac%7B+sqrt%7B2%7D+%7D%7B2%7D+%29%5E2%7D%3D+frac%7B2%7D%7B+frac%7B2%7D%7B4%7D+%7D%3D+frac%7B2%2A4%7D%7B2%7D%3D4+++++ "g'(x)= frac{2}{cos^2x} \ \
g'(- frac{3 pi }{4} )= frac{2}{cos^2(- frac{3 pi }{4} )}= frac{2}{cos^2( frac{3 pi }{4} )}= \ \
= frac{2}{cos^2( pi - frac{ pi }{4} )}= frac{2}{(-cos frac{ pi }{4} )^2}= \ \
= frac{2}{(- frac{ sqrt{2} }{2} )^2}= frac{2}{ frac{2}{4} }= frac{2*4}{2}=4")
г)
![h(x)= frac{1+4x}{x+3} \ \
h'(x)= frac{(1+4x)'(x+3)-(1+4x)(x+3)'}{(x+3)^2}= frac{4(x+3)-(1+4x)}{(x+3)^2}= \ \
= frac{4x+12-1-4x}{(x+3)^2}= frac{11}{(x+3)^2} \ \
h'(-2)= frac{11}{(-2+3)^2}=11](https://tex.z-dn.net/?f=h%28x%29%3D+frac%7B1%2B4x%7D%7Bx%2B3%7D+%5C++%5C+%0Ah%27%28x%29%3D+frac%7B%281%2B4x%29%27%28x%2B3%29-%281%2B4x%29%28x%2B3%29%27%7D%7B%28x%2B3%29%5E2%7D%3D+frac%7B4%28x%2B3%29-%281%2B4x%29%7D%7B%28x%2B3%29%5E2%7D%3D+%5C++%5C+%0A%3D+frac%7B4x%2B12-1-4x%7D%7B%28x%2B3%29%5E2%7D%3D+frac%7B11%7D%7B%28x%2B3%29%5E2%7D+%5C++%5C+%0Ah%27%28-2%29%3D+frac%7B11%7D%7B%28-2%2B3%29%5E2%7D%3D11++++++ "h(x)= frac{1+4x}{x+3} \ \
h'(x)= frac{(1+4x)'(x+3)-(1+4x)(x+3)'}{(x+3)^2}= frac{4(x+3)-(1+4x)}{(x+3)^2}= \ \
= frac{4x+12-1-4x}{(x+3)^2}= frac{11}{(x+3)^2} \ \
h'(-2)= frac{11}{(-2+3)^2}=11")
2.
![f(x)=x^3-6x^2 \
f'(x)=3x^2-12x \ \
g(x)= frac{ sqrt{x} }{3}= frac{1}{3} sqrt{x} \
g'(x)= frac{1}{6 sqrt{x} } \ \ \
f'(x)*g'(x)=0 \
(3x^2-12x)* frac{1}{6 sqrt{x} }=0](https://tex.z-dn.net/?f=f%28x%29%3Dx%5E3-6x%5E2+%5C+%0Af%27%28x%29%3D3x%5E2-12x+%5C++%5C+%0Ag%28x%29%3D+frac%7B+sqrt%7Bx%7D+%7D%7B3%7D%3D+frac%7B1%7D%7B3%7D+sqrt%7Bx%7D++%5C+%0Ag%27%28x%29%3D+frac%7B1%7D%7B6+sqrt%7Bx%7D+%7D+%5C++%5C++%5C+%0Af%27%28x%29%2Ag%27%28x%29%3D0+%5C+%0A%283x%5E2-12x%29%2A+frac%7B1%7D%7B6+sqrt%7Bx%7D+%7D%3D0++++ "f(x)=x^3-6x^2 \
f'(x)=3x^2-12x \ \
g(x)= frac{ sqrt{x} }{3}= frac{1}{3} sqrt{x} \
g'(x)= frac{1}{6 sqrt{x} } \ \ \
f'(x)*g'(x)=0 \
(3x^2-12x)* frac{1}{6 sqrt{x} }=0")
ОДЗ: x>0
1) 3x²-12x=0
3x(x-4)=0
x=0 - не подходит по ОДЗ
x=4
2)
нет решений.
Ответ: 4.
а)
б)
в)
g(x)=2tgx
г)
2.
ОДЗ: x>0
1) 3x²-12x=0
3x(x-4)=0
x=0 - не подходит по ОДЗ
x=4
2)
нет решений.
Ответ: 4.
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад