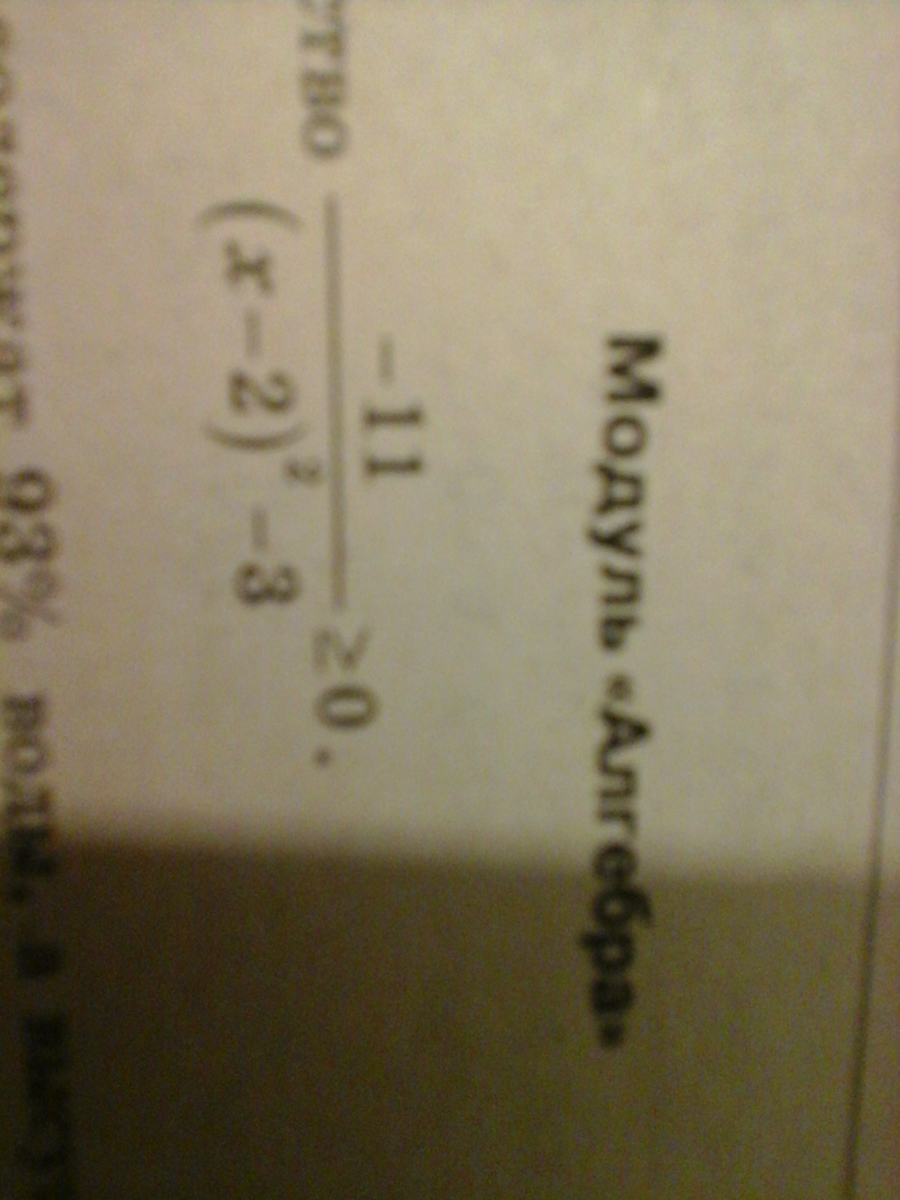Ответы
Ответ дал:
0
Так как числитель всегда меньше 0, то чтобы дробь была положительной, знаменатель тоже должен быть меньше 0
(x-2)^2-3<0
(x-2-корень(3))(х-2+корень(3))<0
Нужно рассматривать два варианта:
1) (х-2-корень(3))>0 и (х-2+корень(3))<0
x>2+корень(3) и х<2-корень(3)
х=(-бесконечность; 2-корень(3))U(2+корень(3); + бесконечность)
2) (х-2-корень(3))<0 и (х-2+корень(3))>0
x<2+корень(3) и х>2-корень(3)
х=(2-корень(3); 2+корень(3))
Объединяя эти два интервала получим
х=(-бесконечность; + бесконечность)
ОДЗ: (х-2)^2-3 не равно 0
х-2 не равно корень(3)
х не равен (2+корень(3))
(x-2)^2-3<0
(x-2-корень(3))(х-2+корень(3))<0
Нужно рассматривать два варианта:
1) (х-2-корень(3))>0 и (х-2+корень(3))<0
x>2+корень(3) и х<2-корень(3)
х=(-бесконечность; 2-корень(3))U(2+корень(3); + бесконечность)
2) (х-2-корень(3))<0 и (х-2+корень(3))>0
x<2+корень(3) и х>2-корень(3)
х=(2-корень(3); 2+корень(3))
Объединяя эти два интервала получим
х=(-бесконечность; + бесконечность)
ОДЗ: (х-2)^2-3 не равно 0
х-2 не равно корень(3)
х не равен (2+корень(3))
Ответ дал:
0
что-то я перемудрил((
Ответ дал:
0
(х-2)^2<3
Ответ дал:
0
Х<(2+корень(3))
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад