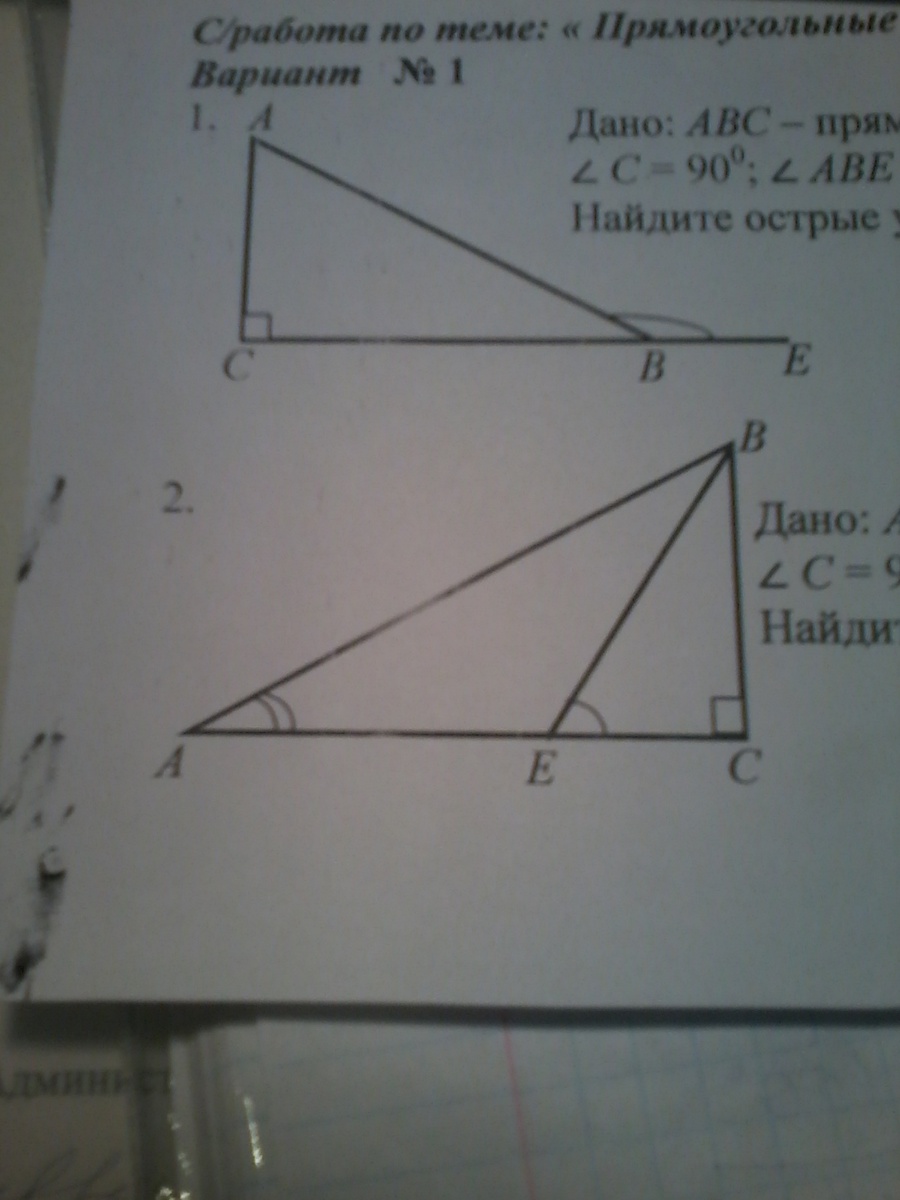
Дано: ABC - прямоугольный треугольник, угол C = 90°, угол A = 30°, угол BEC = 60°, EC = 7 см.
Найдите AE.

<AEB=120°, как смежный с <BEC. Тогда в треугольнике АВЕ <ABE= 180°-120°-30°=°30 (по сумме углов треугольника).  В прямоугольном треугольнике АВС <B=60° (так как <A=30° - дано). Значит <CBE=30° (60°-30°=30°). В прямоугольном треугольнике СВЕ против угла 30° лежит катет ЕС=7см (дано). Значит гипотенуза ЕВ=14см.
Треугольник АЕВ равнобедренный, так как <A=<АВЕ=30°. Следовательно, АЕ=ЕВ=14см.
Ответ: АЕ=14см.

спасибо большое