В прямоугольном треугольнике АВС угол С = 90 градусов, СD - высота треугольника АС=5см, СВ=10см. Чему равно отношение площадей треугольников АСD и CDB
Ответы
Ответ дал:
1
Т,к. <ADC=<BCA=90 градусов и <DAC - общий, то треугольники ADC и ABC подобны. Т.к. <BDC=<BCA=90 градусов и <ABC - общий, то треугольники DBC и ABC подобны. Т.к. треугольник ADC подобен треугольнику ABC и треугольник DBC подобен треугольнику ABC, то треугольники ADC и DBC также подобны, и при том их коэффициент подобия равен BC/AC=10/5=2. Т.к. отношение площадей подобных треугольников равно коэффициенту подобия в квадрате, то 2^2=4=Sdbc/Sadc=> Sdbc=4Sadc.
Ответ: Sdbc=4Sadc.
Ответ: Sdbc=4Sadc.
Приложения:
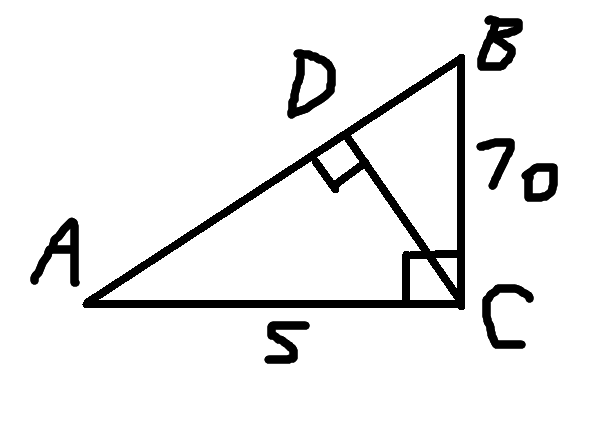
Похожие вопросы
1 год назад
1 год назад
1 год назад
6 лет назад
8 лет назад