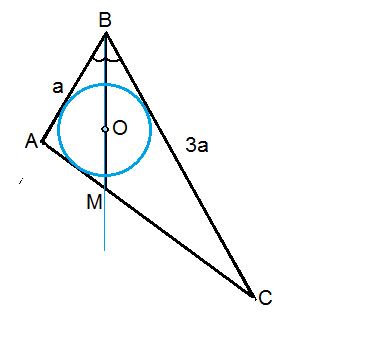
в треугольнике авс угол в равен 60 градусов bc=3ab, и в него же вписана окружность с центром o.Луч BO пересекает сторону AC в точке M.Найдите CM

Примем АВ=а, тогда ВС=3а.  
По т.косинусов:   
АС²=АВ²+ВС²-2АВ*ВС*cos ∠AB   
АС²=а²+9а²-6а²*1/2  
АС²=7а²  
АС=а√7 или АВ√7 ( см. выше)   
О-центр вписанной окружности и лежит на биссектрисе угла АВС  Биссектриса треугольника делит противоположную сторону в  отношении длин прилежащих сторон.⇒    
АМ:МС=АВ:ВС   
АМ:МС=1:3   
АС =1+3=4 части.  
 МС=АС:4*3  
СМ=(3АВ√7):4=0,75 АВ√7