гайти площадь фигуры огоантченными линиями y=x^2-x
y=-x^2-3x напишите хотя бы просто решение, без графика

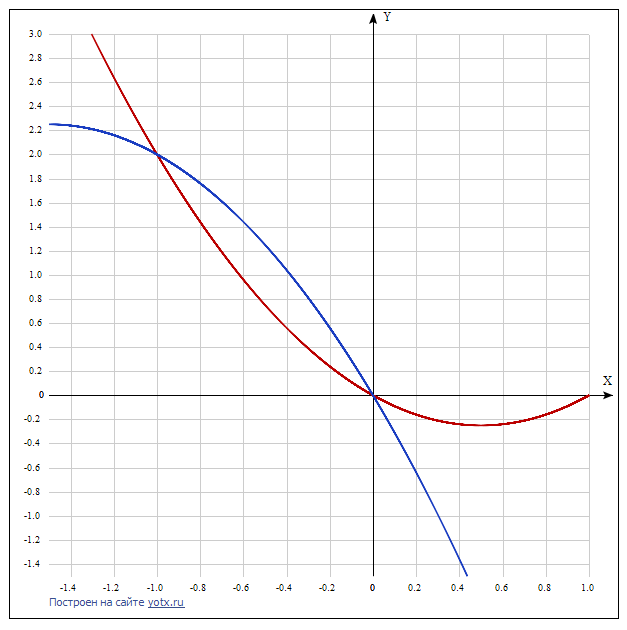
 В самом начале находим точки пересечения линий, решая уравнение
х² - х = - х²-3х
2х²+2х = 0
2х (х+1) = 0
х=0, х=-1. Это пределы интегрирования.
 Сверху будет линия у = -х²-3х.
Поэтому площадь равна интегралу от -1 до 0 от функции (-х²-3х)-(х²-х) =( -2х² -2х)dx.
Первообразная будет 2/3 x³-x². Подстановка от -1 до 0.
2/3*0³ -0²-(2/3-1) = 1/3. Это ответ.