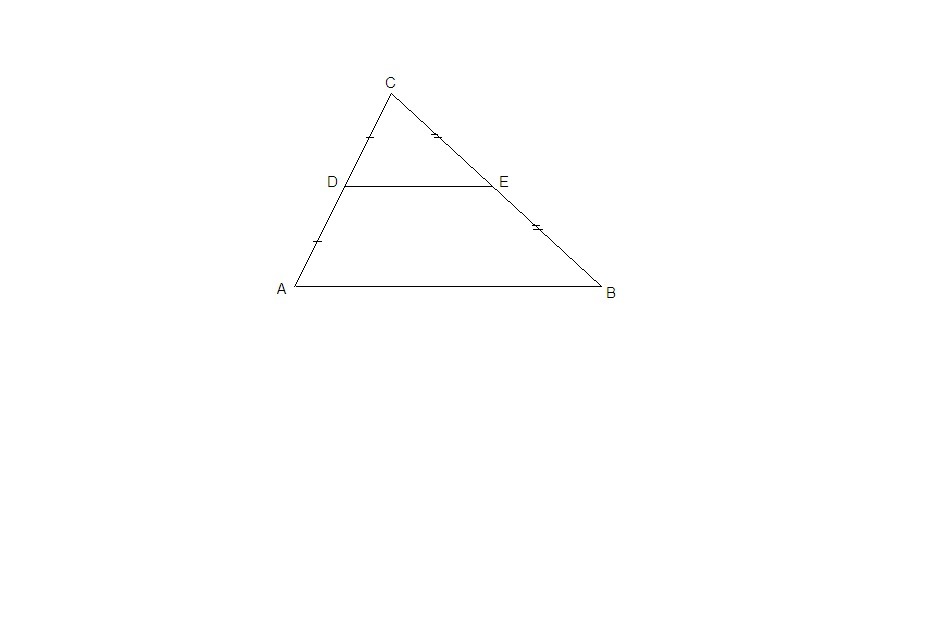
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 1. Найдите площадь треугольника ABC.

AC = 2DC, BC = 2EC, ∠С - общий для треугольников АВС и DEC, значит
ΔАВС подобен ΔDEC по двум пропорциональным сторонам и углу между ними.

k = AC/DC = 2

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Sabc : Sdec = k² = 4

Sabc = 4 · Sdec = 4 · 1 = 4