Куб пересечен плоскостью, проходящей через середины трёх его ребер, исходящих из одной вершины. Площадь сечения равна 16√3. Какова площадь поверхности шара вписанного в этот куб?

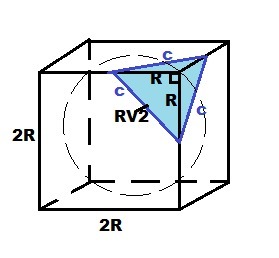
Шар с радиусом R вписан в куб.
Тогда ребро куба равно диаметру шара 2R.

Секущая плоскость проходит через середины рёбер куба, отсекая от каждой грани прямоугольный равнобедренный треугольник с катетами R.
Тогда гипотенуза такого треугольника равна  с = R√2 .
Три гипотенузы - это стороны равностороннего треугольника, который получился в сечении.
Площадь равностороннего треугольника в сечении 
     по условию равна   16√3 ⇒

R² = 32
Площадь поверхности шара
S = 4πR² = 4π*32 = 128π