Высота правильного треугольника равна 9см. Вычислите площадь круга, ограниченного описанной около треугольника окружностью.
Ответы
Ответ дал:
0
висота= a*(√3/2)
a= 9/ (√3/2)
радіус = a*(√3/3)
R=(9/ (√3/2))* (√3/3)=9/2=4,5
S=pi*R²
S= pi*20,25=3,14*20,25=63,585 (см²)
Відповідь: 63,585 см²
Приложения:
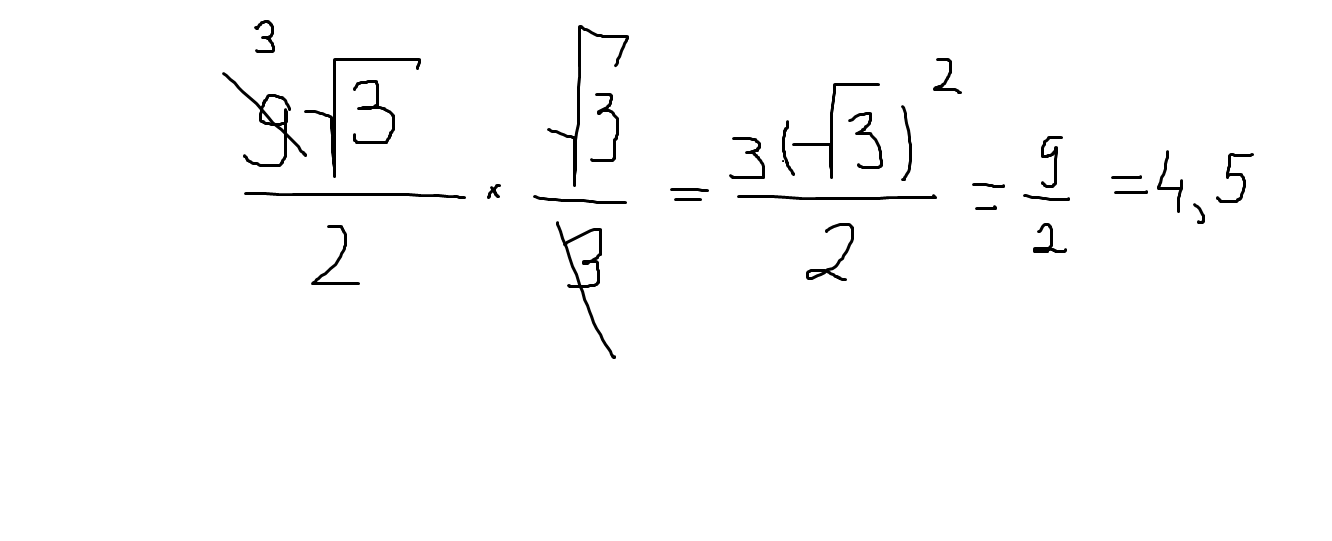
Ответ дал:
0
В правильном или равностороннем треугольнике высота совпадает с медианой. Поэтому первая замечательная точка треугольника совпадает с точкой пересечения высот (медиан). Медианы делятся точкой пересечения в отношении 1:2. Т.е. расстояние от точки пересечения (О) до любой из вершин равно 9:3х2 = 6см. Эта точка является центром описанной вокруг треугольника окружности.
Площадь круга равна пи*R^2 или 36пи.
Приложения:
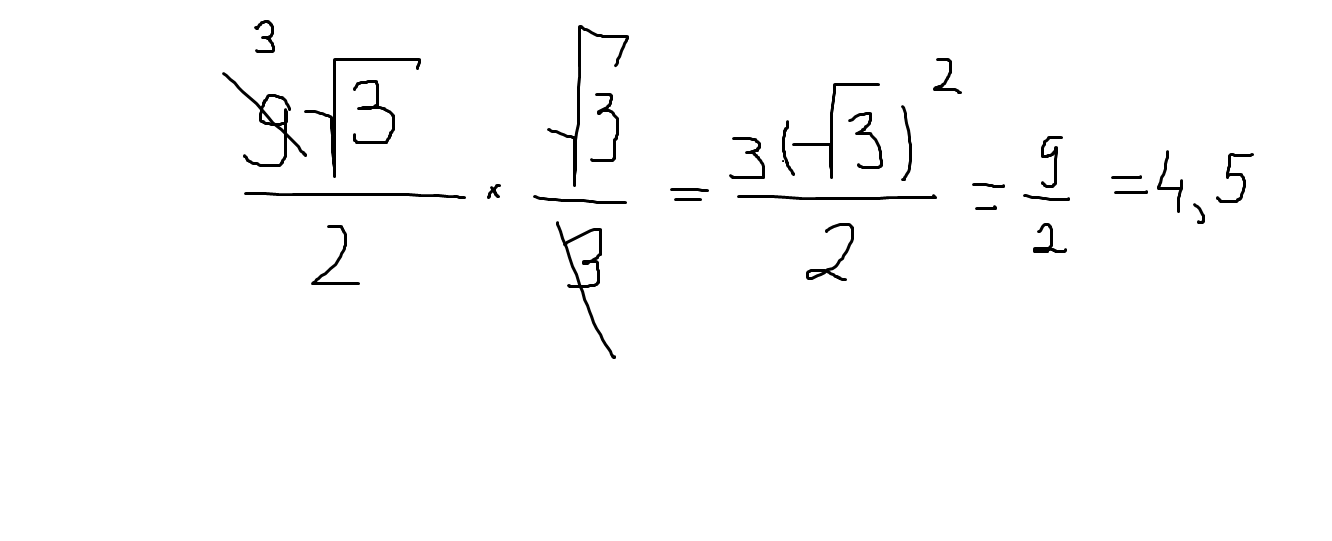
Похожие вопросы
2 года назад
7 лет назад
10 лет назад
10 лет назад