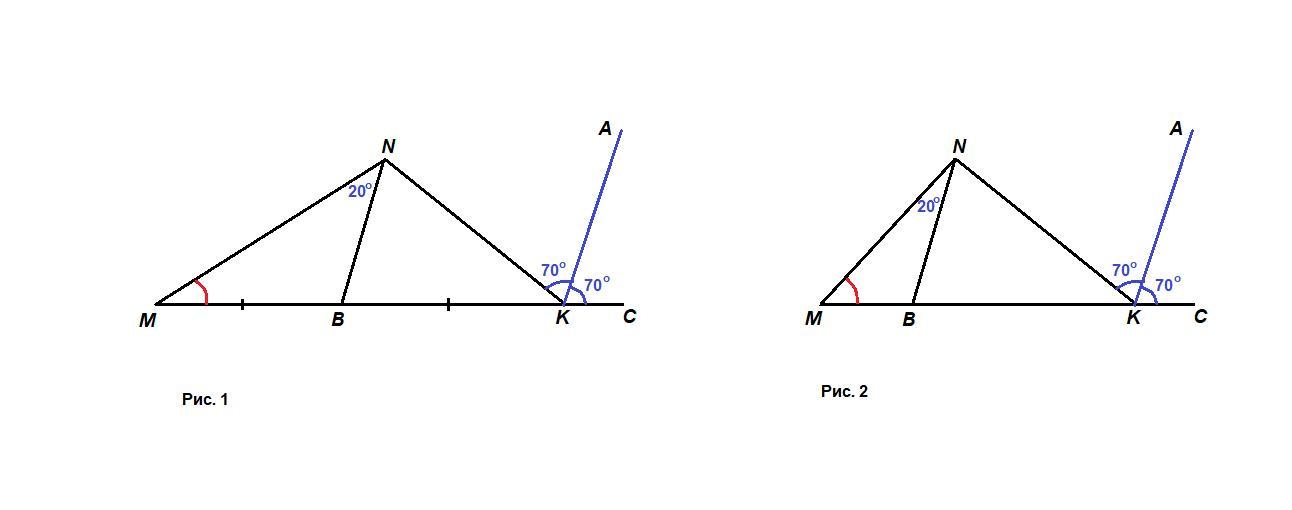
внешний угол треугольника mnk при вершине k равен 140 градусов а биссектриса этого угла параллельна медиане nb найдите градусную меру угла m если угол mnb равен 20 градусов.определите вид треугольника bnk
Ответы
n c
m b k a
угол nbk=cka=1/2nka=1/2*140=70
угол nmb=180-mnb-nbm, где угол nbm=180-nbk=180-70=110, угол nmb=180-20-110=50
в тр-ке bnk угол nbk=70, nkb=140-70=70 (смежный угол равен сумме несмежных с ним углов). Значит тр-к равнобедренный
Ответ:
∠M = 50°
ΔBNK равнобедренный
Объяснение:
∠NBK = ∠AKC = 70° как соответственные при пересечении BN║АК секущей ВК,
∠BNK = ∠NKA = 70° как накрест лежащие при пересечении BN║АК секущей NК,
Значит ΔBNK равнобедренный с основанием NB.
∠NBK = ∠BNM + ∠M, так как внешний угол треугольника равен сумме двух внутренних, не смежных с ним, тогда
∠М = 70° - 20° = 50°
P.S. Из решения получается, что ∠MNK = 90°, но тогда NB - медиана, проведенная к гипотенузе, а тогда она равна половине гипотенузы, т.е. NB = MB = BK. Но тогда треугольники NBM и NBK равнобедренные, с основаниями NM и NK, но это не соответствует данным задачи. Следовательно, NB - это не медиана. И тогда правильным будет рисунок 2.