• Предмет: Алгебра
  • Автор: 411e
  • Вопрос задан 2 года назад
< >

Найдите интеграл, напишите решение на листочке и сфотографируйте пожалуйста, а то через символы сложно понять

Приложения:

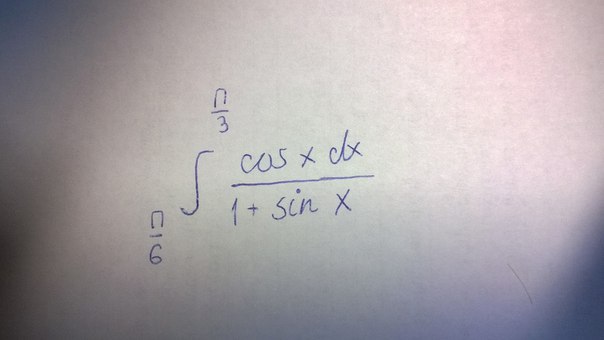
Ответы

Ответ дал: sirca
1
\int\limits^{ \frac{ \pi }{3} }_{ \frac{ \pi }{6} } { \frac{cosx}{1+sinx} } \, dx =|u=1+sinx, du=cosxdx|= \int\limits^{ \frac{ \pi }{3} }_{ \frac{ \pi }{6} } { \frac{du}{u} } = lnu|_{ \frac{ \pi }{6} }^{ \frac{ \pi }{3} }=\\\\=ln(1+sinx)|_{ \frac{ \pi }{6} }^{ \frac{ \pi }{3} }=ln(1+sin \frac{ \pi }{3} )-ln(1+sin \frac{ \pi }{6} )=\\\\=ln(1+ \frac{ \sqrt{3} }{2} )-ln(1+0.5)=ln(1+ \frac{ \sqrt{3} }{2} )-ln(1.5)
Похожие вопросы
Математика
1 год назад
Зробіть вираз будь ласка
Математика
1 год назад
4. Вычисли. 1/5 от 45 1/6 от 48 9 см - это 1/2 от 3 см - это четверть от ... 10 см - это половина от ... 5 см - это треть от ...​
Английский язык
1 год назад
Вставьте предлог This is a piece .... jewerly
Английский язык
1 год назад
Помогите пожалуйста с задачами
Українська література
6 лет назад
Хто і що впливає на життя людини?
История
6 лет назад
Коротка характеристика українського барокко​
Математика
8 лет назад
Строители возводили 6 этажей дома за 8 месяцев. Сколько этажей в новом доме, если после возведения фундамента его строили еще 2 года?
Математика
8 лет назад
Решите: 8^(2x+5)=(1/32)