ДАЮ 80 БАЛЛОВ.
В четырехугольнике ABCD биссектриса угла А перпендикулярна биссектрисе угла В. Биссектриса угла А пересекает сторону ВС в точке М, а биссектриса угла В сторону AD в точке N. Докажите , что ABMN - ромб.

В четырехугольнике ABCD биссектриса угла А перпендикулярна биссектрисе угла В. Биссектриса угла А пересекает сторону ВС в точке М, а биссектриса угла В сторону AD в точке N.
Докажите , что ABMN - ромб
-------- 
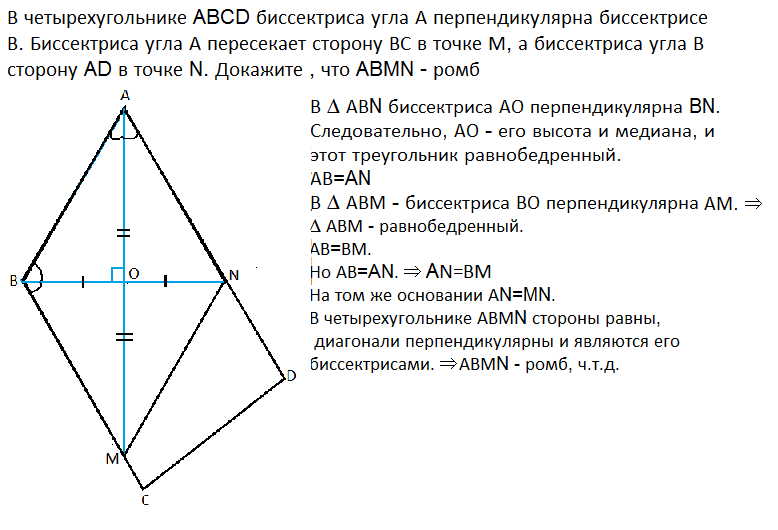
В ∆ АВN биссектриса АО перпендикулярна BN. ⇒,  
АО - его высота и медиана, и этот треугольник равнобедренный.  
АВ=AN  
В ∆ АВМ - биссектриса ВО перпендикулярна АМ. ⇒  
∆ АВМ - равнобедренный.  
АВ=ВМ.  
Но АВ=AN, значит, АN=BM 
 На том же основании АN=MN. 
В четырехугольнике АВМN все стороны равны,  диагонали взаимно перпендикулярны и являются биссектрисами его углов. ⇒  
АВМN - ромб, ч.т.д.

Большое спасибо!

:)