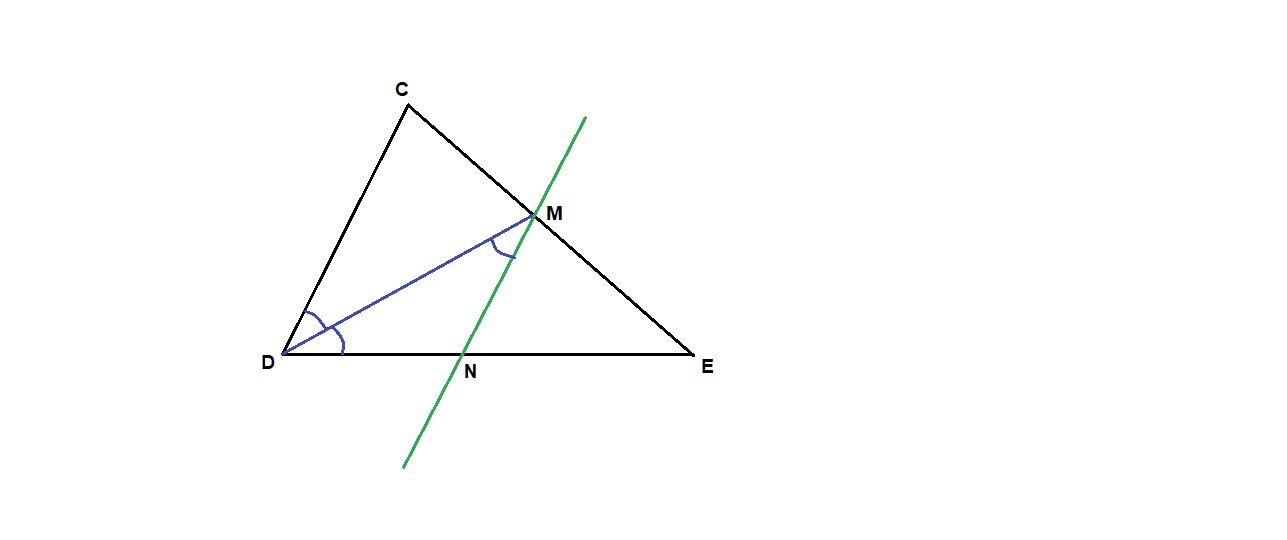
отрезок DM - биссектриса треугольника CDE .через точку м проведена прямая,параллельная стороне CD и пересекающая сторону DE в точке N,найти углы треугольника DMN , если угол CDE равен 68 градусов...ОЧЕНЬ НУЖНО ПОМОГИТЕ
Ответы
Ответ дал:
0
∠CDM = ∠EDM = ∠CDE / 2 = 34°, так как DM - биссектриса угла CDE.
∠NMD = ∠CDM = 34° как накрест лежащие при пересечении параллельных прямых CD и MN секущей DM.
Значит в треугольнике DMN:
∠NDM = ∠NMD = 34°,
Так как сумма углов треугольника 180°, то
∠DNM = 180° - (∠NDM + ∠NMD) = 180° - 34° · 2 = 180° - 68° = 112°
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад