Ответы
Ответ дал:
0
x²-3x+4=x+1
x²-4x+3=0
(x-3)(x-1)=0
x1=1 x2=3

x²-4x+3=0
(x-3)(x-1)=0
x1=1 x2=3
Приложения:
Ответ дал:
0
Совсем не такое решение!
Ответ дал:
0
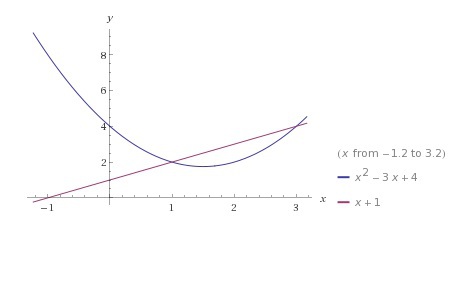
График такой
Ответ дал:
0
решать можно многими способами
Ответ дал:
0
http://znanija.com/task/18026417 реши
Ответ дал:
0
зачем решать ее, если тут решено?
Ответ дал:
0
Найдем пределы интегрирования
x²-3x+4=x+1
x²-4x+3=0
x1+x2=4 U x1*x2=3
x1=1 U x2=3
Фигура ограничена сверху прямой,а снизу параболой
S=S(x+1-x²+3x-4)dx=S((-x²+4x-3)dx=-x³/3+2x²-3x|(3-1)=
=-9+18-9+1/3-2+3=1 1/3
x²-3x+4=x+1
x²-4x+3=0
x1+x2=4 U x1*x2=3
x1=1 U x2=3
Фигура ограничена сверху прямой,а снизу параболой
S=S(x+1-x²+3x-4)dx=S((-x²+4x-3)dx=-x³/3+2x²-3x|(3-1)=
=-9+18-9+1/3-2+3=1 1/3
Приложения:

Похожие вопросы
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад