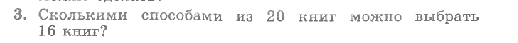Предмет: Алгебра
Автор: FastPlay
Вопрос задан 9 лет назад

Пожалуйста. Решите задачу на скриншоте.

Приложения:

Ответы

Ответ дал: sedinalana

Если ограничений нет, то это число сочетаний из 20 по 16 и равно
20!/(4!*16!)=(16!*17*18*19*20)/(16!*1*2*3*4)=4845

Ответ дал: Келай

Нужно найти количество сочетаний из 20 по 16.
$C= frac{n!}{(n-m)!*m!} = frac{20!}{(20-16)!*16!}= frac{20*19*18*17}{4*3*2*1}=4845$
Ответ: 4845 способов

Похожие вопросы

Математика

2 года назад

Из двух городов расстояния между которыми 918км выехали навстречу друг друг два скорых поезда. Скорость первого поезда 65км/ч . Кокова скорость другого поезда если поезда встретились через 6ч

Русский язык

2 года назад

Найди название еды к ключевому слову трапеза

Қазақ тiлi

7 лет назад

помогите пожалуйста задание на фото даю 50 балов

Русский язык

7 лет назад

Дели столица Индии какой падеж

Литература

9 лет назад

сочинение на тему рецепт от скуки

Математика

9 лет назад

Найти значение выражения 6a (во второй степени) - 2a - 1, при a = - 1/4 (дробь)

Информатика

10 лет назад

ОБЪЯСНИТЕ,что такое исполнитель водолей и как он действует???

Физика

10 лет назад

Помогите срочно!!! Какой монохроматический свет больше (меньше) преломляется?