2) В двух ящиках находятся соответственно: в первом – 6 белых и 4 черных, во втором 3 белых и 7 черных шара. Извлечение шара изщ любого ящика равновероятно. Найти вероятность того, что извлечение было произведено из второго ящика, если вынутый шар оказался черным.
Ответы
Ответ дал:
0
РЕШЕНИЕ
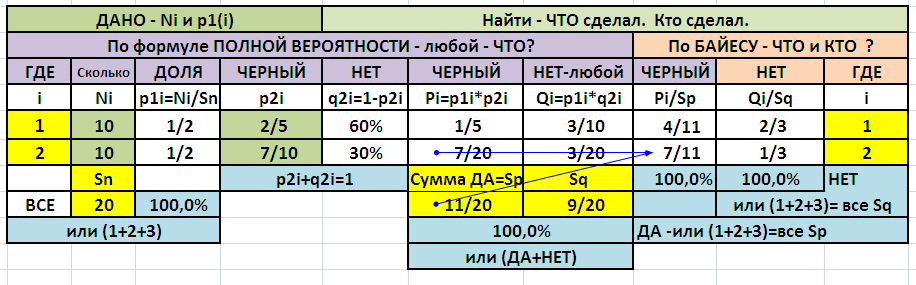
Вероятность вынуть "любой" - р11=р12=0,5
Вероятность вынуть "черный" - р21 = 4/10= 2/5 и р22 = 7/10
Теперь событие А - вынуть И любой И черный = сумма произведений вероятностей
Р(А) = 1/2 * 2/5 + 1/2 * 7/10 = 1/5 + 7/20 = 11/20 - всего "черный"
Откуда - по формуле Байеса - для первой - (1/5):(11/20) = 4/11 ~ 0.3636
для второй - = (1/5) : (11/20) = 7/11 = 06363 ~ 63.6% - ОТВЕТ
Дополнительно - таблица с расчетом
Вероятность вынуть "любой" - р11=р12=0,5
Вероятность вынуть "черный" - р21 = 4/10= 2/5 и р22 = 7/10
Теперь событие А - вынуть И любой И черный = сумма произведений вероятностей
Р(А) = 1/2 * 2/5 + 1/2 * 7/10 = 1/5 + 7/20 = 11/20 - всего "черный"
Откуда - по формуле Байеса - для первой - (1/5):(11/20) = 4/11 ~ 0.3636
для второй - = (1/5) : (11/20) = 7/11 = 06363 ~ 63.6% - ОТВЕТ
Дополнительно - таблица с расчетом
Приложения:
Ответ дал:
0
Там нигде нет 1/4. р= 1/2 * 2/5 = 1/5
Ответ дал:
0
а в чем разница в первой и второй формуле Байеса?
Ответ дал:
0
Первая - 36% для первой - не нужна, вторая - 63% в ответ
Ответ дал:
0
В таблице не 5/9, а 11/20
Ответ дал:
0
Таблица уточнена
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад