Ответы
Ответ дал:
0
Найдите все решения неравенства
|3х-у-7|+|2у-5х-3|≤0
т.к |3х-у-7|≥0 и |2у-5х-3|≥0 , то |3х-у-7|+|2у-5х-3|≤0 ⇔
|3х-у-7|+|2у-5х-3|=0 ⇔ 3х-у-7=0 6x-2y=14
2у-5х-3=0 -5x+2y=3 ⇔ x=17 y =3x-7
y=44
проверка
3·17-44-7 =0
2·44-5·17-3=0
ответ: x=17 y =44
|3х-у-7|+|2у-5х-3|≤0
т.к |3х-у-7|≥0 и |2у-5х-3|≥0 , то |3х-у-7|+|2у-5х-3|≤0 ⇔
|3х-у-7|+|2у-5х-3|=0 ⇔ 3х-у-7=0 6x-2y=14
2у-5х-3=0 -5x+2y=3 ⇔ x=17 y =3x-7
y=44
проверка
3·17-44-7 =0
2·44-5·17-3=0
ответ: x=17 y =44
Ответ дал:
0
Спасибо)))
Ответ дал:
0
у этого неравенства только одно решение: (17; 44)
т.к. сумма двух неотрицательных чисел (модуль--число неотрицательное))) не может быть <0 и остается только =0
т.к. сумма двух неотрицательных чисел (модуль--число неотрицательное))) не может быть <0 и остается только =0
Приложения:
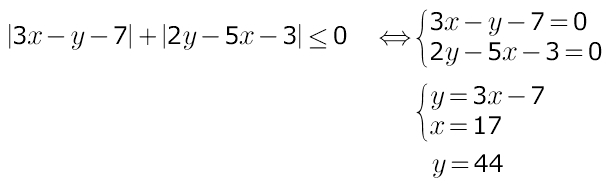
Ответ дал:
0
Спасибо)))
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад