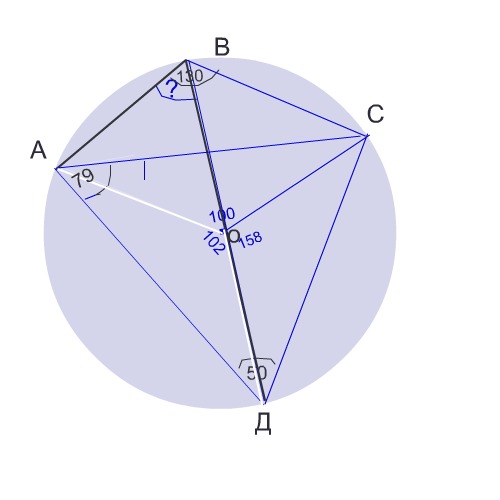
четырёхугольник ABCD вписан в окружность. Угол ABC равен 130 градусам, угол CAD равен 79 градусам. Найдите угол ABD. Ответ дайте в градусах

Задача на вычисление вписанных углов. 

Сделаем рисунок. 

Во вписанном четырехугольнике сумма противоположных углов равна 180°. 

Следовательно,

∠ СДА равен   180°-130°=50°

Центральный ∠АОС  опирающийся на   дугу АВС, равен двум углам СДА  и равен 100°  

По условию ∠ САД равен 79°

Центральный∠ СОД равен 79° ·2=158° 

Так как окружность содержит 360°, центральный

∠ АОД равен  360°-100° -158°=102°

∠ АВД опирается на ту же дугу, что и ∠ АОД, поэтому равен его половине:

∠АВД=102°:2=51°