В треугольнике ABC, где AB=15см,AC=20см, косинус угла равен 0.6. Найдите площадь треугольника. Только подробное решение.
Ответы
Ответ дал:
0
вот решение только так
Приложения:
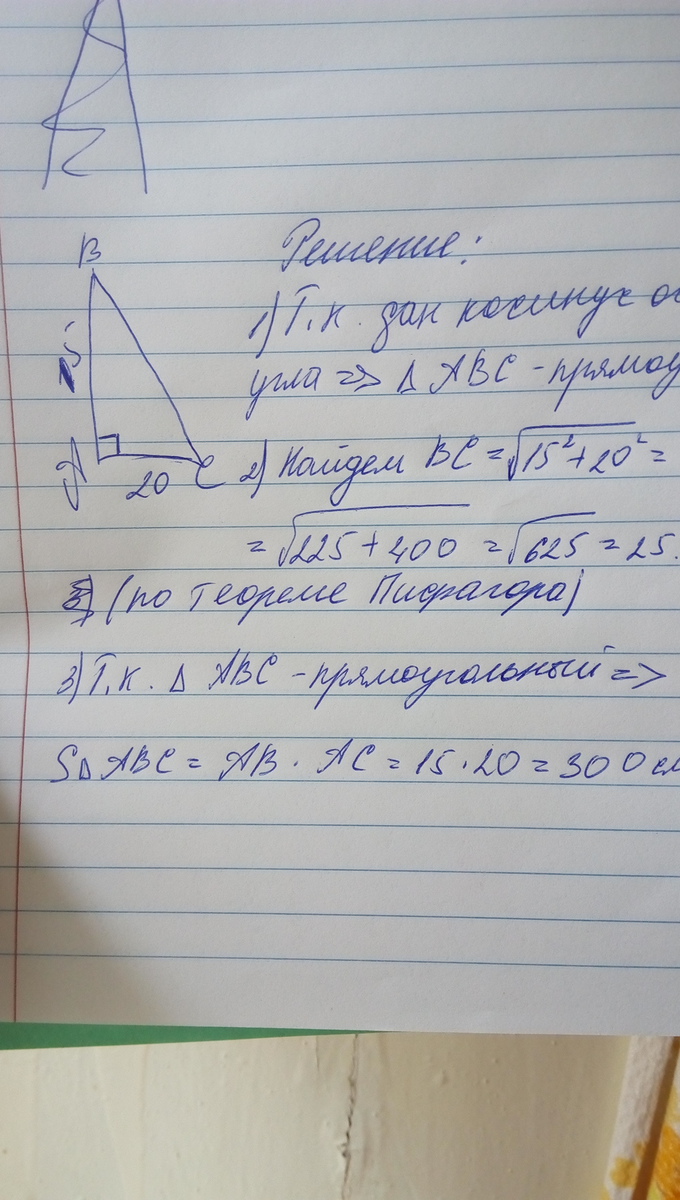
Ответ дал:
0
ок
Ответ дал:
0
а как вставить другую картинку
Ответ дал:
0
еще раз добавь комментарий
Ответ дал:
0
короче острого прямоугольный и см в квадрате
Ответ дал:
0
а все остальное там есть
Ответ дал:
0
Не пиши ответ из прошлого комментария!!! Там неправильно. Если дан косинус острого угла то треугольник прямоугольный??? ЧТО ЗА БРЕД! это неверно, есть два доказательства. Если открыть конец учебника 9 класса и посмотреть градусную меру угла А( учитывая что косинус=0,6), то он приблизительно равен 53 градусам, что уже не сходится . И второе доказательство: если посмотреть в таблицу же( в конце учебника по геометрии 9 кл.) косинус угла 90 градусов= 0, а там дано 0,6. Вот, поэтому я хочу чтобы ты не писала это глупое и неправильное решение.
Приложения:
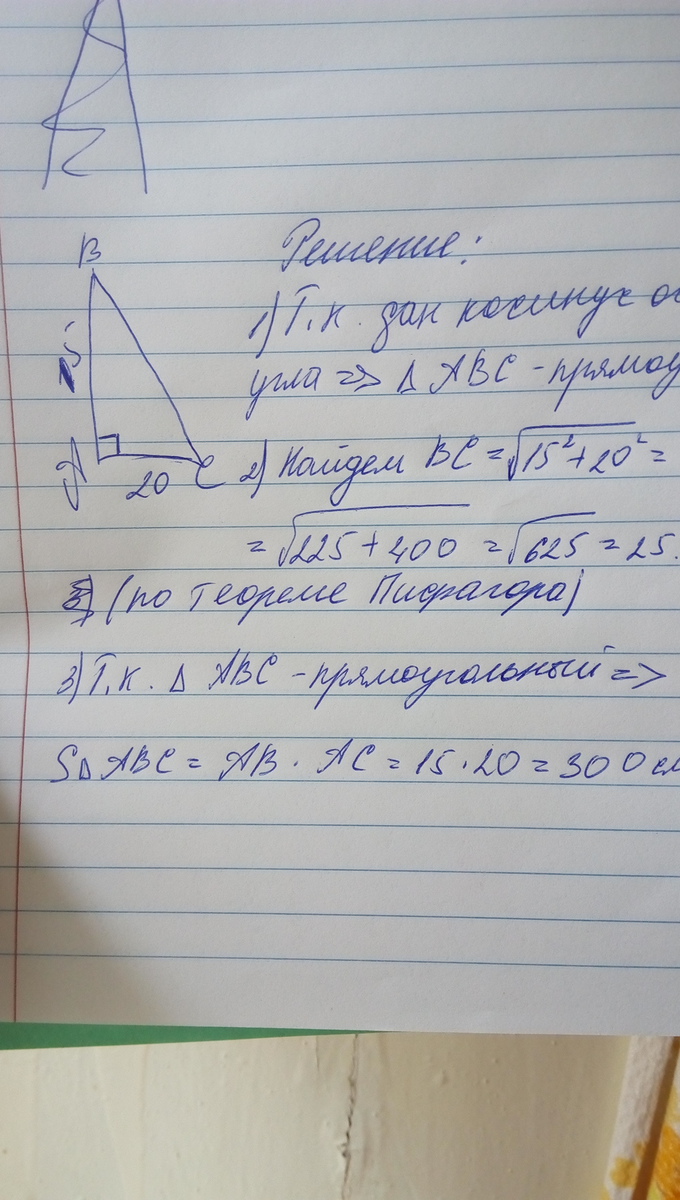
Ответ дал:
0
Давай помогу с задачей. Проводишь высоту BH, тогда треугольник ABH- прямоугольный. CosA=AH/AB => AH=cosA*AB=15*0.6=9 (см). После по т Пифагора BH^2=AB^2-AH^2=225-81=144/ BH=√144=12(cм). Значит Sabc=1/2AC*BH=10*12=120(cм^2).
Похожие вопросы
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад