Постройте график функции и определите при каких значениях m прямая y=m
имеет с графиком одну общую точку.
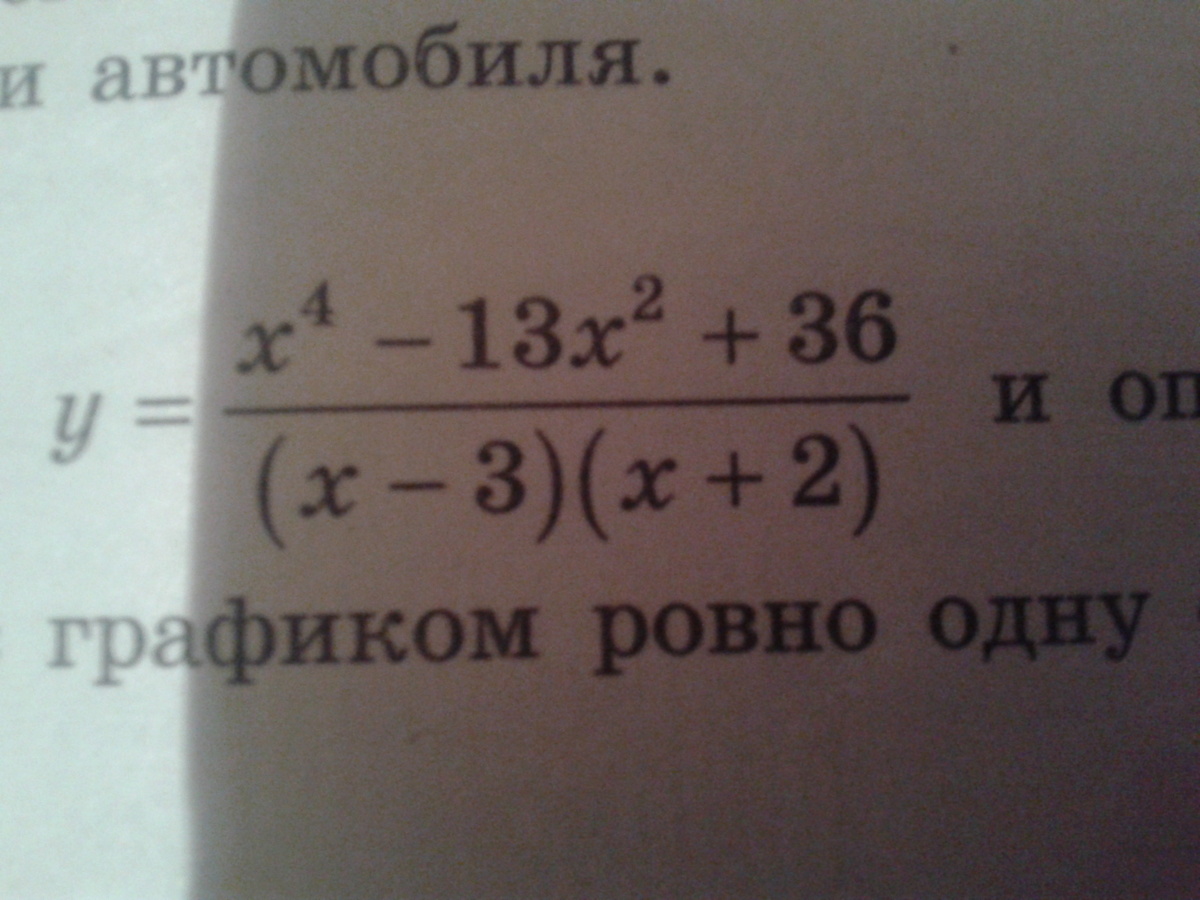
Ответы
Преобразуем числитель
Теперь преобразуем знаменатель
Таким образом, в числителе и знаменателе сокращается и остается функция
, которая является параболой с двумя выколотыми точками: при x=3 и x=-2 (в силу ОДЗ).
Прямая y=m будет иметь одну общую точку при трех значениях m.
Первый случай, когда прямая касается вершины параболы, т.е. при m=-6,25 (для нахождения этого значения надо сначала вычислить абсциссу вершины параболы по формуле , а затем полученное решение подставить вместо x и найти y параболы).
Второй случай, когда прямая пересекает параболу в точке x=3. Подставляя это х в параболу получаем y=m=6.
Третий случай, когда прямая пересекает параболу в точке x=-2. Подставляя это х в параболу получаем y=m=-4.
Ответ: m=-6.25, m=6, m=-4.