Срочно ребята, помогите.
найти объем шара вписанного в конус Образующая конуса наклонена под углом 30 градусов к основанию и равна 4
Ответы
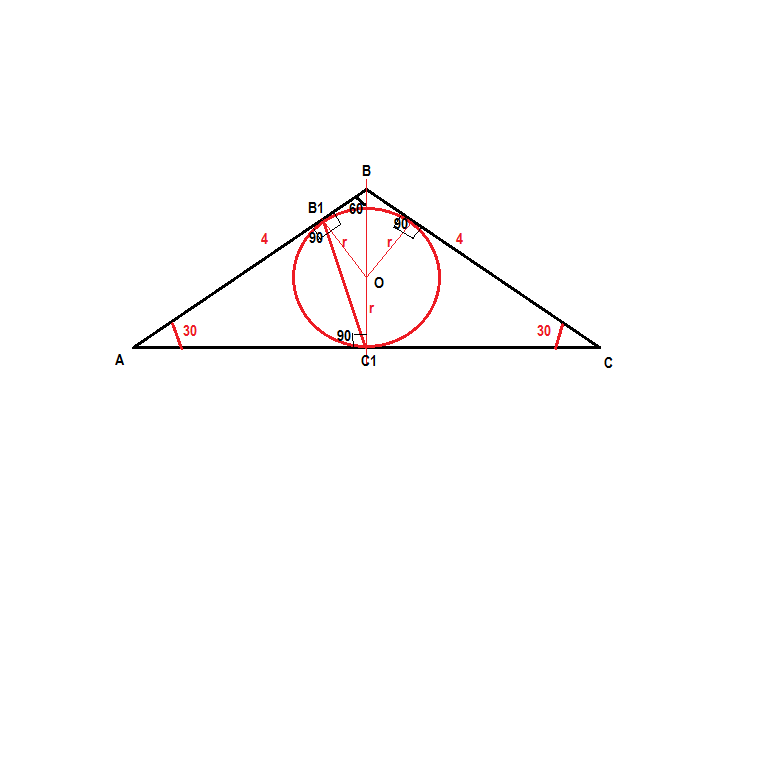
сделаем построение по условию
на рисунке осевое сечение шара и конуса (вертикальный разрез через вершину конуса)
r -радиус вписанной окружности, он же радиус шара вписанного в конус
треугольник АВС -равнобедренный
<A=<C=30 град
<B=180 -<A-<C=180-30-30=120 град
BC1 - высота,биссектриса,медиана
<B1BO=<ABC1=120/2=60
AC1=AB*cos30 =4*√3/2=2√3
OB1=r -перпендикуляр в точке касания
OС1=r -перпендикуляр в точке касания
AB1 = AC1 по теореме об отрезках касательных
значит AB1 = AC1=2√3
тогда BB1=AB-AB1=4-2√3
в прямоугольном треугольнике B1BO
tg<B1BO =OB1/BB1
OB1 =BB1 *tg<B1BO
подставим известные значения
r = (4-2√3) *tg60 =4√3-6 - радиус шара
объем шара
V =4/3*pi*r^3== 4/3*pi*(4√3-6)^3
= 32pi*(26√3-45)
= (832√3-1440)pi
= 832√3pi-1440pi
** ответ на выбор