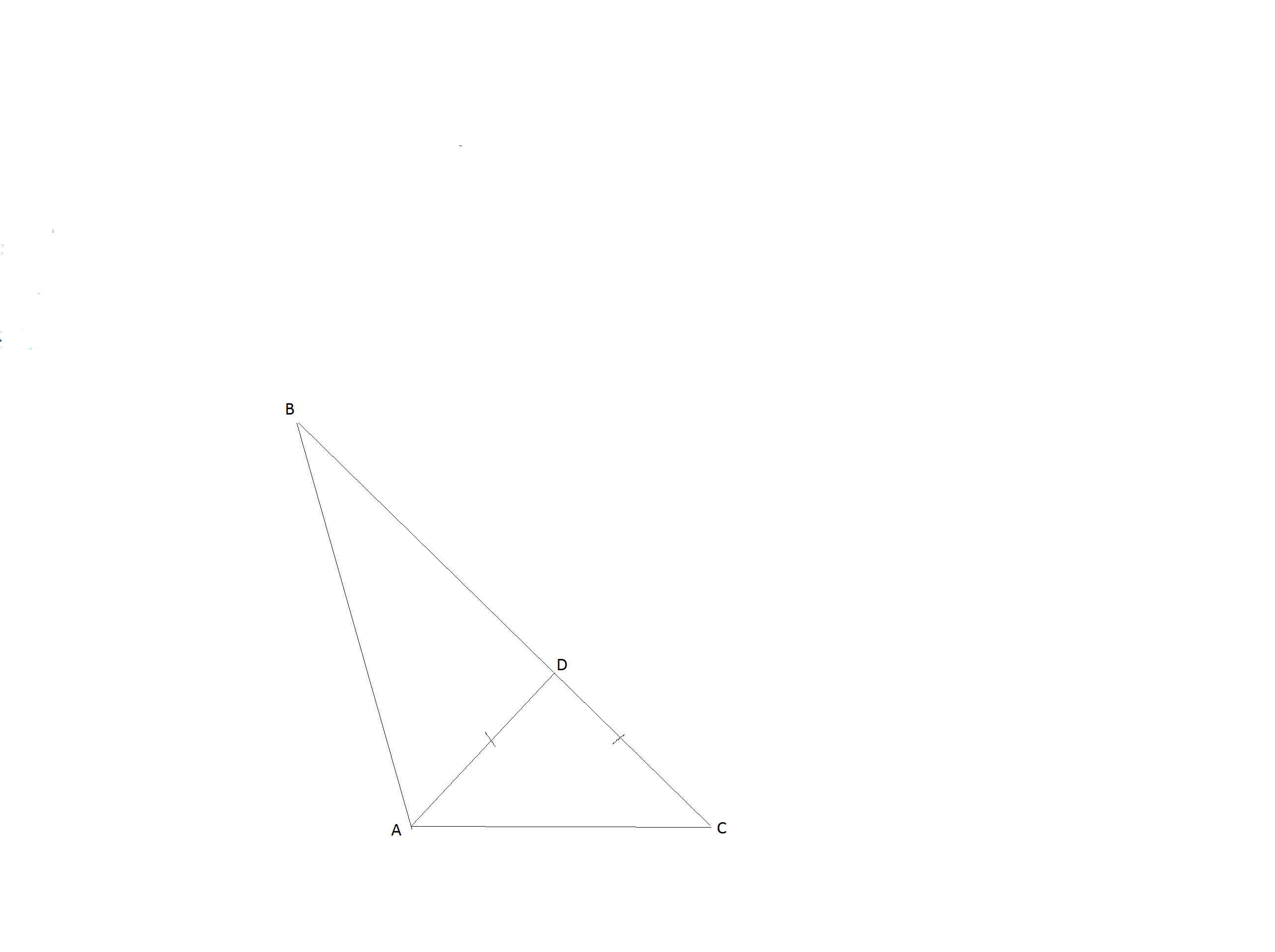
Внутри треугольника ABC  к стороне BC проведена прямая AD так, что получился равнобедренный треугольник ADC с основанием AC. найдите дляну основания AC если периметры треугольников ABCи ABD равны соответственно 39 см и 27 см

Внутри треугольника ABC к стороне BC проведена прямая AD так, что получился равнобедренный треугольник ADC с основанием AC.
Найдите длину основания AC, если периметры треугольников ABC и ABD

равны соответственно 39 см и 27 см

Решение

Рассмотрим оба треугольника.

Если из треугольника АВС вырезать АС, то, так как АD=DС, получим периметр треугольника АВD.
Р АВС - Р АВD= АС
АС=39-27=12 см

Если трубуется, есть и второй вариант решения:

Запишем периметры обоих треугольниокв в виде суммы их сторон

Р ᐃ АВС=АВ+ВС+АС=39 см

а так ВС=ВD+DС, то

Р ᐃ АВС=АВ+ВD+DС+АС=39 см

Периметр ᐃ АВD=АВ+ВD+АD=27 см

Так как АD=DС, то можем записать

Р ᐃ АВD=АВ+ВD +DС =27 см

Составим систему:

|АВ+ВD +DС+АС =39
|АВ+ВD+DС=27___________ Умножим это уравнение на -1 и сложим уравнения.

|АВ+ВD +DС+АС =39
| -АВ - ВD -DС = - 27 
                     АС=12 cм