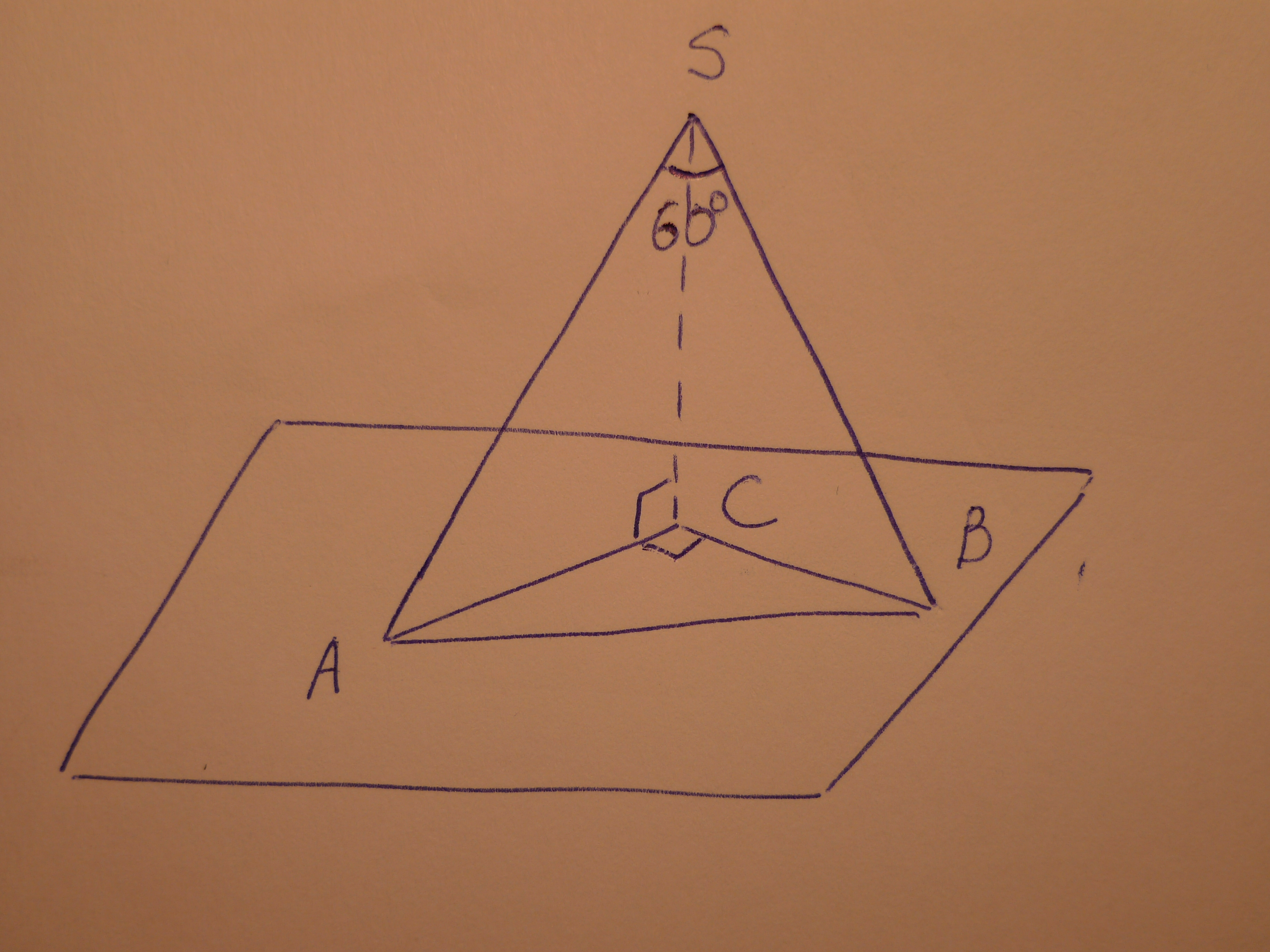
из точки к плоскости проведены 2 наклонные угол между ними 60 градусов, а угол между их проекциями равен 90 градусов. Найдите расстояние от точки до плоскости если длинны этих наклонных равны 3 корень из двух

SA = SB = 3√2, значит ΔASB -- равнобедренный.
Равнобедренный треугольник с углом при вершине 60° является равносторонним. Поэтому АВ = SA = SB = 3√2.
Из равенства наклонных, опущенных из одной точки, следует равенство их проекций: АС = ВС.
ΔACB -- равнобедренный прямоугольный. Значит:

Расcтояние от точки S до плоскости АСВ равно длине перпендикуляра SC.
По теореме Пифагора: