• Предмет: Математика
  • Автор: kate86157
  • Вопрос задан 9 лет назад
< >

Интегралы! Помогите пожалуйста! Это очень срочно!
Для того чтобы увеличить изображение, кликните на него (если кто не знает как его увеличивать) Даю 42 бала!

Приложения:

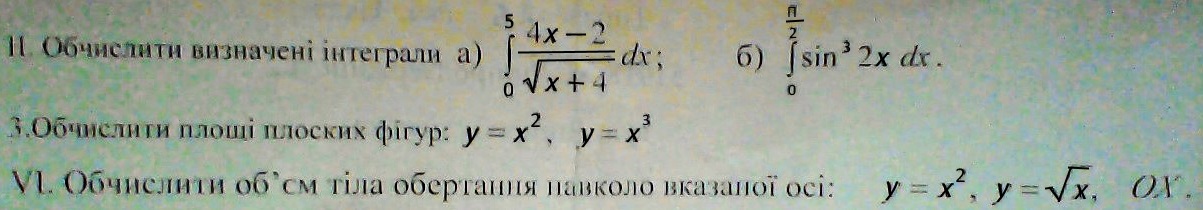
Ответы

Ответ дал: NNNLLL54
0
1)quad intlimits^5_0 {frac{4x-2}{sqrt{x+4}}} , dx =[t^2=x+4,; x=t^2-4,; dx=2t, dt,t_1=2; ,; t_2=3]=\\= intlimits^3_2 {frac{4t^2-18}{t}}cdot 2t , dt =2cdot ({frac{4t^3}{3}-18t)|_2^3=2cdot (frac{4cdot 3^3}{3}-18cdot 3)-

-2cdot (frac{4cdot 2^3}3}-18cdot 2)=2(36-54)-2(frac{32}{3}-36)=frac{44}{3}\\2)quad intlimits^{frac{pi}{2}}_0 {sin^32x} , dx = intlimits^{frac{pi}{2}}_0 {(1-cos^22x)sin2x} , dx =\\= intlimits^{frac{pi}{2}}_0 {sin2x} , dx - frac{1}{2}intlimits^{frac{pi}{2}}_0 {cos^22x} , d(cos2x) =\\=-frac{1}{2}cos2x|_0^{frac{pi}{2}}+frac{1}{2}cdot frac{cos^32x}{3}|_0^{frac{pi}{2}}=-frac{1}{2}(-1-1)+frac{1}{6}(-1-1)=

=1-frac{1}{3}=frac{2}{3}

3)quad S= intlimits^1_0 {(x^2-x^3)} , dx =(frac{x^3}{3}-frac{x^4}{4})|_0^1=frac{1}{3}-frac{1}{4}=frac{1}{12}\\4)quad V=pi intlimits^1_0 {((sqrt{x})^2-(x^2)^2)x} , dx =pi intlimits^1_0 {(x-x^4)} , dx =\\=pi (frac{x^2}{2}-frac{x^5}{5})|_0^1=pi (frac{1}{2}-frac{1}{5})=pi cdot frac{3}{10}=0,3pi
Ответ дал: kate86157
0
Спасибо ОГРОМНОЕ!!!!
Похожие вопросы
Химия
2 года назад
Во сколько раз возрастает скорость прямой реакции H2+ O2= H2O, если увеличить концентрацию водорода в три раза? пожалуйста объясните подробнее!!!!!
Алгебра
2 года назад
При каком условии уравнение (a-2)x=x+1 не имеет решений ? 7 класс
Алгебра
7 лет назад
Выберите выражения, которые являются одночленами.
Українська мова
7 лет назад
Українська мова. Даю 15 баллів.
Физика
9 лет назад
на какой угол поворачивается земля вокруг своей оси за 1 мин. ответ выразите в минутах.
Обществознание
9 лет назад
Синонимы страха, имя одного из сыновей Бога войны
Геометрия
10 лет назад
В равнобедренном треугольнике высоты,проведенные к основанию и к боковой стороне равны соответственно 10 и 12 см.Найдите длину основания. очень нужно,помогите(((
Химия
10 лет назад
Даны схемы реакций: 1)Гидроксид алюминия - оксид алюминия+вода 2)Гидроксид бария+соляная кислота - хлорид бария+вода 3)Фосфорная кислота+цинк - фосфат цинка+водород 4)оксид азота(4)+вода+кислород -