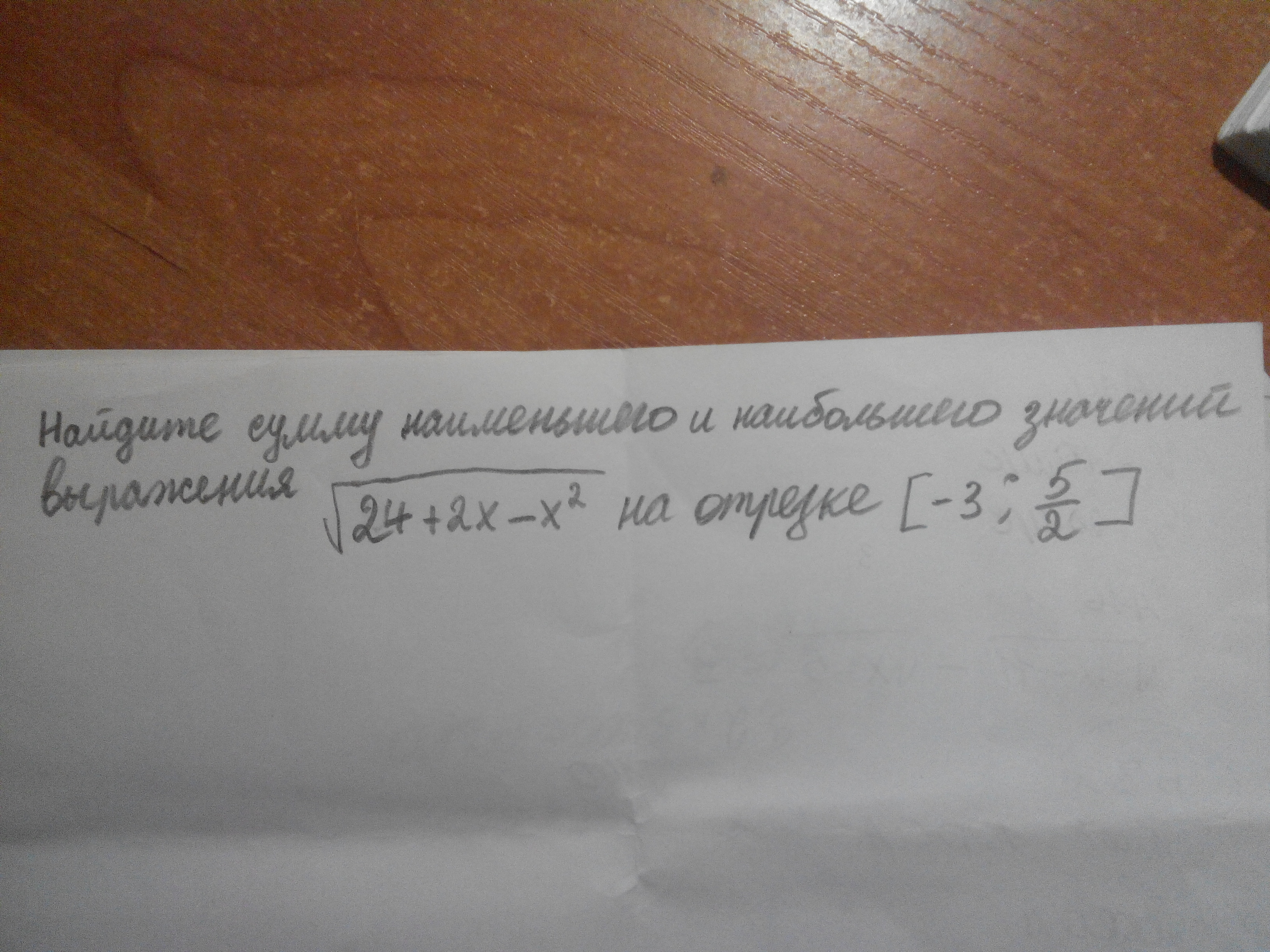Ответы
Ответ дал:
0
минимальное и максимальное значение может быть на границах и в точке экстремума
обозначим корень через у
y=√(24+2x-x²)=√(24+1-1+2x-x²)=√(25-(x²-2x+1))=√(25-(x-1)²)
в точке x=1 экстремум
максимальное значение y=y(1)=√25=5
значения на границах интервалов
y(-3)=√(24-6-9)=√9=3
у(5/2)=√(24+5-25/4)=√(29-6,25)=√22,75≈4,76
min y =3
max y =5
сумма 3+5=8
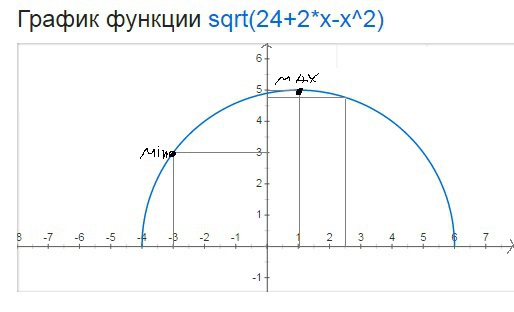
иллюстрация на картинке
обозначим корень через у
y=√(24+2x-x²)=√(24+1-1+2x-x²)=√(25-(x²-2x+1))=√(25-(x-1)²)
в точке x=1 экстремум
максимальное значение y=y(1)=√25=5
значения на границах интервалов
y(-3)=√(24-6-9)=√9=3
у(5/2)=√(24+5-25/4)=√(29-6,25)=√22,75≈4,76
min y =3
max y =5
сумма 3+5=8
иллюстрация на картинке
Приложения:
Ответ дал:
0
√(24+2x-x²) x∈[-3;2,5]
(√(24+2x-x²))`=(2-2x)/2√(24+2x-x²)=(2(1-x)/2√(24+2x-x²)=(1-x)/√(24+2x-x²)=0
1-x=0
x=1∈[-3;2,5]
y(-3)=√(24-6-9)=√9=3 наим
y(1)=√(24+2-1)=5 наиб
y(2,5)=√(24+5-6,25)=√(22,75)≈4,769
3+5=8
Ответ 8
(√(24+2x-x²))`=(2-2x)/2√(24+2x-x²)=(2(1-x)/2√(24+2x-x²)=(1-x)/√(24+2x-x²)=0
1-x=0
x=1∈[-3;2,5]
y(-3)=√(24-6-9)=√9=3 наим
y(1)=√(24+2-1)=5 наиб
y(2,5)=√(24+5-6,25)=√(22,75)≈4,769
3+5=8
Ответ 8
Приложения:

Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад