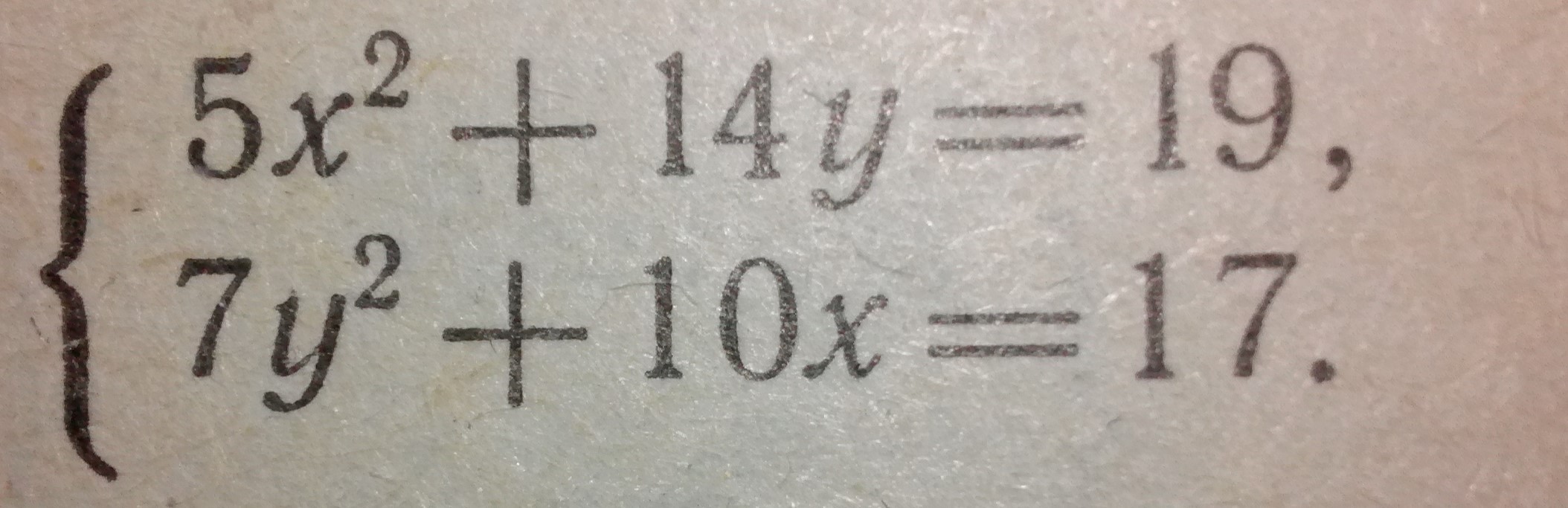решите систему уравнений

Сложим почленно и вычтем почленно получим систему:

Выделяем полные квадраты:

Смотрим на последнее уравнение 5(x-1)² = 7(y-1)². Данное равенство будет верно когда в левой и правой его части будут нули.
⇒ х = 1, у = 1.
Эти же числа удовлетворяют и первому уравнению последней системы.
Ответ: (1; 1).

там еще корни есть

Если использовать способ подстановки, то получаем уравнение четвёртой степени.
Из второго уравнения х = (17-7у²)/10.
Подставив в первое, получаем:
49у⁴-238у²+280у-91 = 0.
Корней у этого уравнения 3:
х₁ = 1,                   у₁ = 1.
х₂ = -1-2√(7/5),      у₂ = -1-2√(5/7)
х₃ = 2√(7/5)-1,       у₃ = 2√(5/7)-1.

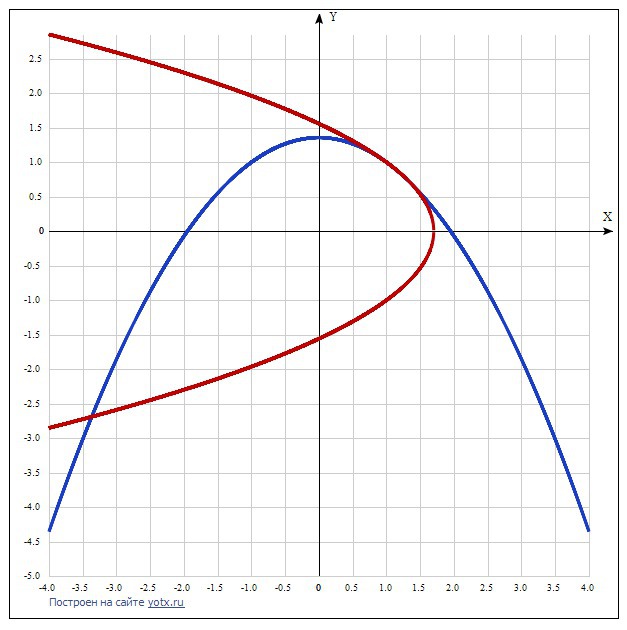
Графически - это точки пересечения двух парабол, повёрнутых относительно друг друга на 90 градусов.
График дан в приложении, но 2 точки пересечения плохо видны - линии накладываются.