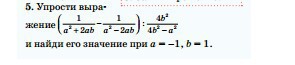помогите пожалуйста дам 10 баллов

Вот решение этого примера

при  а=1  ; b= -1


упростим выражение в скобках:
1/(а²+2ab)  -   1/ (a²-2ab) =
вынесли общий множитель в знаменателях:
= 1/ (а*(а+2b) )        -   1/( a*(a-2b)) =
к общему знаменателю:
= (а-2b  - (a+2b))   /  ( a (a-2b)(a+2b)) =
= (a-2b-a-2b)  /   (a(a-2b)(a+2b)) =
= -4b / (a (a-2b)(a+2b) )

деление:
-4b /   ( a(a-2b)(a+2b) )  ÷     (4b²/ (4b²-a²)) =
из второй дроби делаем обратную (переворачиваем, меняем знак на умножение) и раскладываем разность квадратов:
= -4b / (a(a-2b)(a+2b) )     *        ((2b-a)(2b+a))  / 4b²  =
=  -4b /  (a(a-2b)(a+2b)      *      (-1(a-2b)(a+2b) / 4b² =
сокращаем:
= -1  / а         *      -1/ b  =        1/ab

при а= 1 ;  b= -1
1/ (1  *  (-1 ) )  =     - 1

Обнови страницу - будут дроби

не получается

Сейчас ответ по простому напишу, бывает , что с телефонов не открывается редактор

хорошо

спасибо большое