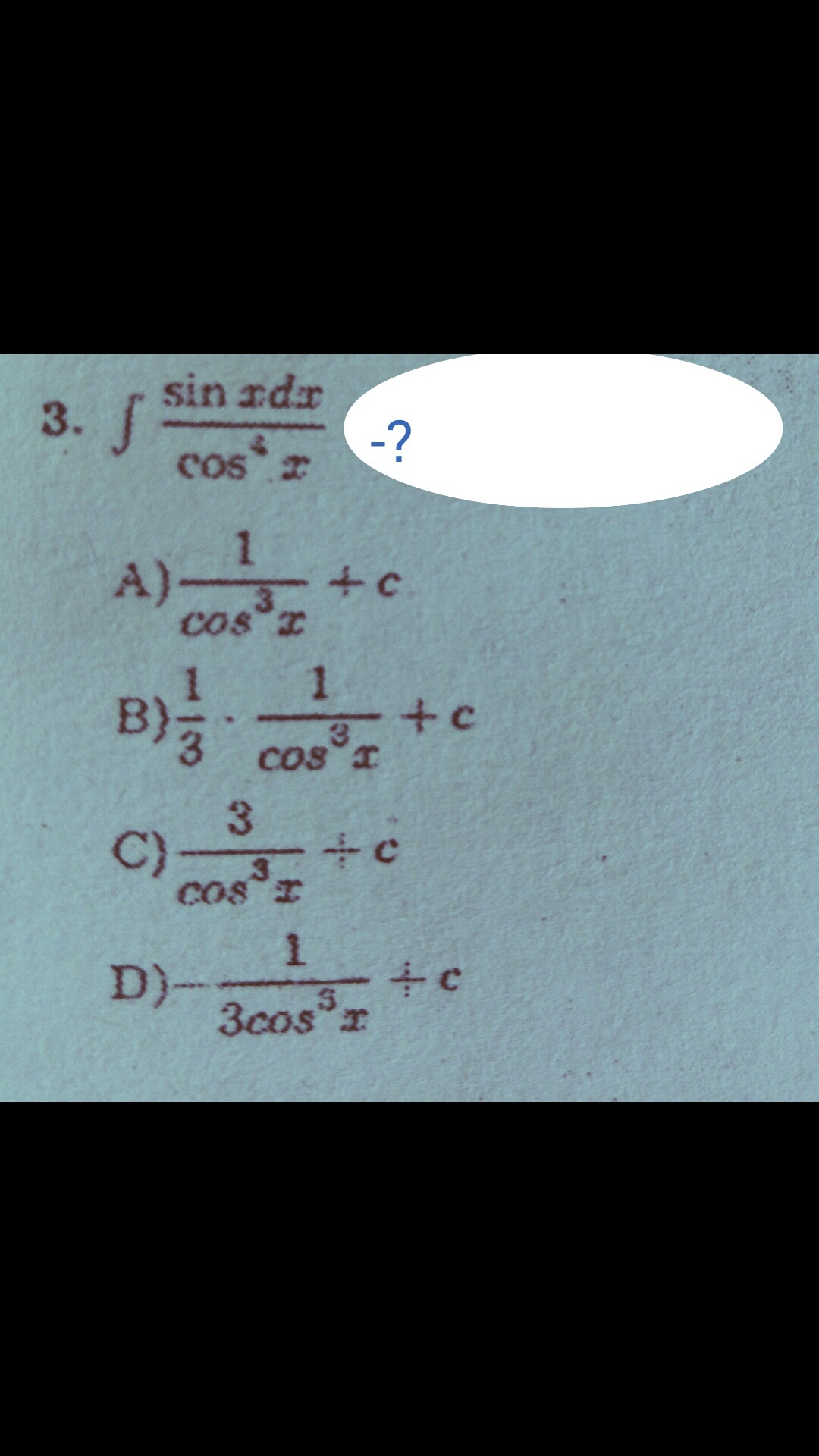Ответы
Ответ дал:
0
[tex] intlimits(sinx/cos^4x)dx =⇒
sinx/cos⁴x=tgx·sec³x;
u=secx⇒du=tgx·secx·dx;⇒
[tex] intlimits {tgxsec^3x} , dx = intlimits {u ^{2} } , du=u³/3+C =
=sec³x/3+C
sinx/cos⁴x=tgx·sec³x;
u=secx⇒du=tgx·secx·dx;⇒
[tex] intlimits {tgxsec^3x} , dx = intlimits {u ^{2} } , du=u³/3+C =
=sec³x/3+C
Ответ дал:
0
Вроде,так......................
Приложения:

Ответ дал:
0
$sinz*d*cosz)/(cos^4z*sinz) откуда взялса cosz/sinz
Ответ дал:
0
Вы про вторую запись после =?
Ответ дал:
0
Таким образом мы подводим косинус под знак дифференциала.Есть правило,чтобы подвести какое-то выражение под знак дифференциала,надо разделить исходное выражение на производную требуемого нам.
Ответ дал:
0
Т.к. мы хотим чтобы под дифференциалом у нас стоял cos x,а не просто х,то исходную дробь просто делим на производную cosx,которая равна - sin x
Ответ дал:
0
Поэтому синус и появляется в знаменателе
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад
10 лет назад